Ordres de magnitud

Aquesta lliçó explica com classificar funcions segons la seva velocitat de creixement quan la variable tendeix a l'infinit, utilitzant ordres de magnitud. Veurem per què aquest concepte és fonamental en informàtica per analitzar l'eficiència dels algorismes i entendre els límits pràctics del tractament de grans volums de dades.

Comparació de funcions per a valors grans

La precisió és inherent a les matemàtiques: no és el mateix $3x^2+2x+1$ que $3.01x^2+2x^{1.25}+3$. Ara bé, en moltes ocasions, la diferència entre aquestes dues funcions és poc rellevant. Al cap i a la fi, si aquestes funcions són aproximacions de mesures experimentals o provenen de simplificacions en models teòrics, ja contenen un cert grau d'error. Per tant, per què preocupar-se dels seus detalls?

Quan només ens interessa com creix una funció quan la seva variable tendeix a l'infinit, podem classificar les funcions segons la seva velocitat de creixement utilitzant ordres de magnitud.

Per exemple, per a $f(n)=3n^2+2n+23$, podem dir que $f$ creix quadràticament perquè, quan $n$ és molt gran, el terme dominant és $3n^2$ i els altres termes ($2n$ i $23$) es tornen insignificants en comparació. De fet, el factor $3$ també es pot ignorar en aquest context, ja que només ens interessa l'ordre de magnitud i no la constant multiplicativa exacta. Per tant, podem dir que $f(n)$ és de l'ordre d'$n^2$.

Igualment, per a $g(n)=5n^3+0.1n^2+1000$, podem dir que $g$ creix cúbicament perquè el terme dominant és $5n^3$ i els altres termes es tornen insignificants quan $n$ és molt gran. Així, podem dir que $g(n)$ és de l'ordre d'$n^3$.

De la mateixa manera, per a $h(n)=3\log (n+1)+1/n$, podem dir que $h$ creix logarítmicament perquè el terme dominant és $3\log (n+1)$ i el terme $1/n$ es torna insignificant quan $n$ és molt gran. Igualment, per a valors grans d'$n$, $\log (n+1)$ es comporta de manera similar a $\log n$. Per tant, podem dir que $h(n)$ és de l'ordre de $\log n$.

Entre les tres funcions, podem establir l'ordre de creixement següent:

$$h\ll f\ll g$$

on el símbol $\ll$ indica que la funció de l'esquerra creix molt més lentament que la funció de la dreta quan $n$ tendeix a l'infinit.

Ordres de magnitud comuns

En informàtica hi ha alguns ordres de magnitud especialment habituals:

Ordre de magnitud	Descripció
$1,5,12,{10}^6$	Constant
$\approx \log n$	Logarítmic
$\approx n$	Lineal
$\approx n\log n$	Quasilineal
$\approx n\sqrt{n}$	Superlineal
$\approx n^2$	Quadràtic
$\approx n^3$	Cúbic
$\approx n^c$	Polinòmic
$\approx c^n$	Exponencial
$\approx n!$	Factorial

La gràfica següent mostra una comparació visual entre alguns d'aquests ordres de magnitud per a petits valors d'$n$:

I la gràfica següent mostra una comparació visual entre alguns d'aquests ordres de magnitud per a valors més grans d'$n$:

Mentre que per a valors petits d'$n$ les diferències entre els ordres de magnitud poden no ser tan evidents, a mesura que $n$ creix, les diferències es fan extremadament pronunciades i dramàtiques.

Temps d'execució aproximats

A continuació es mostra una taula amb els temps d'execució aproximats per a diferents ordres de magnitud, assumint que una operació elemental triga 1 nanosegon (ns):

Funció	Temps per n = 10³	Temps per n = 10⁴	Temps per n = 10⁵
${\log }_{2}n$	10 ns	13.3 ns	16.6 ns
$\sqrt{n}$	31.6 ns	100 ns	316 ns
$n$	1 µs	10 µs	100 µs
$n{\log }_{2}n$	10 µs	133 µs	1.7 ms
$n^2$	1 ms	100 ms	10 s
$n^3$	1 s	16.7 min	11.6 dies
$n^4$	16.7 min	116 dies	3171 anys
$2^n$	$3.4\times {10}^{284}$ anys	$6.3\times {10}^{2993}$ anys	$3.2\times {10}^{30086}$ anys

Aquesta taula il·lustra com els temps d'execució creixen de manera radicalment diferent segons l'ordre de magnitud. Mentre que els algorismes logarítmics i lineals es mantenen tractables fins i tot per a valors grans d'$n$, els algorismes exponencials esdevenen completament impracticables molt ràpidament.

La següent taula (extreta de Algorithm Design per Jon Kleinberg i Éva Tardos, Addison Wesley 2006) mostra els temps d'execució aproximats per a diferents ordres de magnitud, assumint que una operació elemental triga 1 microsegon (µs), i posa de manifest quin és el límit pràctic per a cada ordre de magnitud en aplicacions de big data:

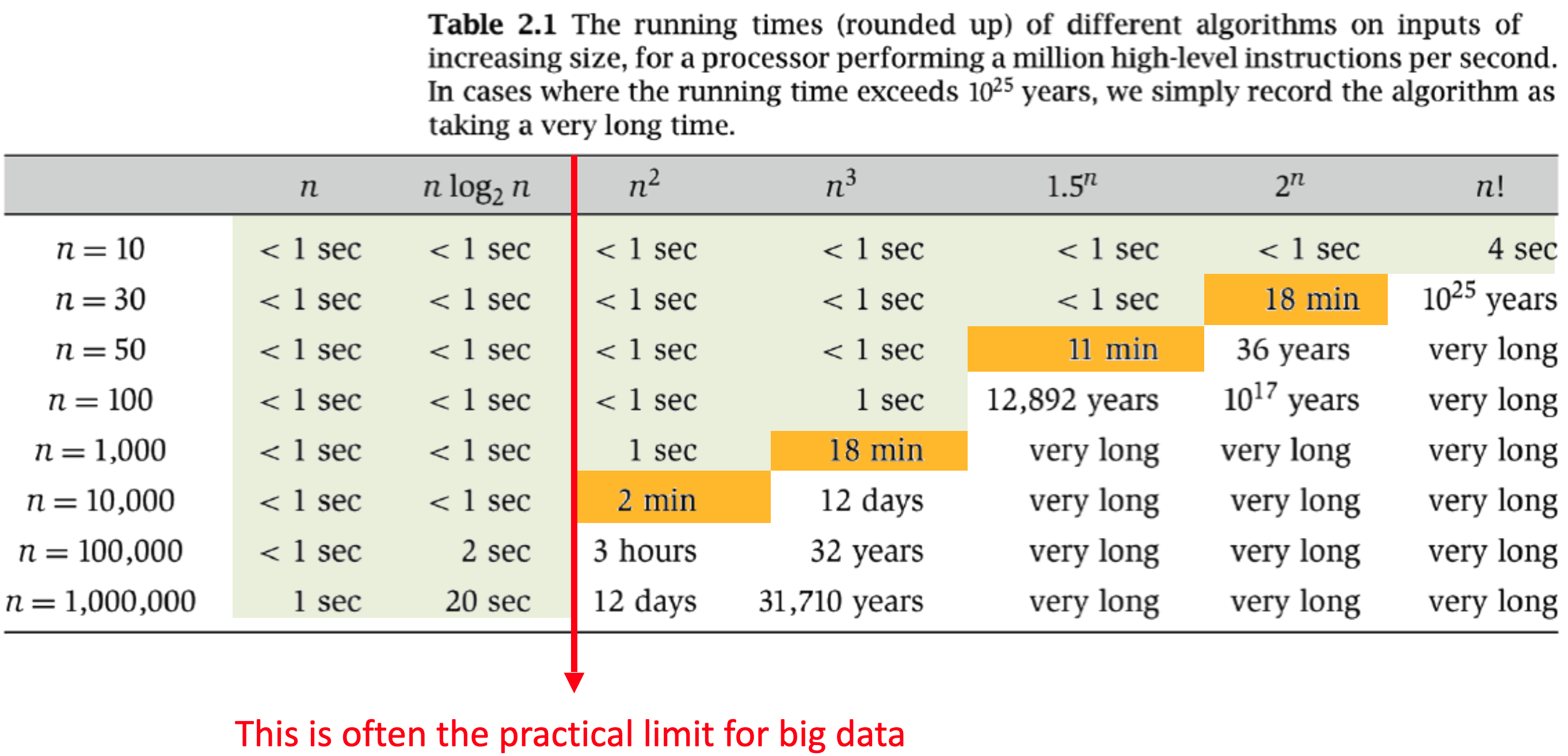
Fixeu-vos que ni tan sols una millora d'un factor 10 en la velocitat dels computadors permetrà tractar conjunts de dades gaire més grans quan l'ordre de magnitud és elevat. L'única alternativa real és disposar d'algorismes més eficients, amb ordres de magnitud més baixos. Aquest fet explica per què la recerca d'algorismes eficients és un dels problemes centrals de la informàtica.

Jordi Petit
Lliçons.jutge.org
© Universitat Politècnica de Catalunya, 2025