Aplicació: Càlcul de la distància euclidiana entre dos punts

Aquesta lliçó mostra com escriure un programa que calculi la distància euclidiana entre dos punts donats.

Enunciat del problema

Es vol un programa que, donats dos punts, calculi la seva distància euclidiana. Recordeu que la distància euclidiana $d$ entre dos punts $(x_1,y_1)$ i $(x_2,y_2)$ es pot calcular amb la fórmula:

$$d=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}.$$

Aquí en teniu la interpretació geomètrica:

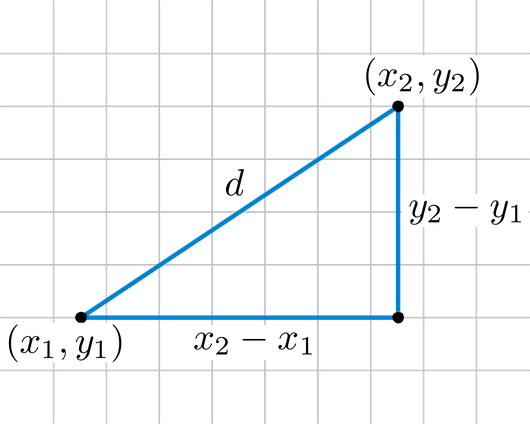
Iep!

Penseu com resoldre el problema abans de continuar llegint!

Solució

El primer pas per resoldre qualsevol problema és identificar quines són les seves entrades, quines són les seves sortides i quina relació tenen entre elles. En aquest cas:

• De l'enunciat del problema, queda clar que hi ha dues entrades: els dos punts. Ara bé, com es representen aquests punts? Doncs, amb les seves coordenades. Per tant, les entrades són quatre nombres reals x1, y1, x2 i y2.

• Igualment, queda clar que la sortida és un nombre real d que representa la distància euclidiana entre els dos punts.

La relació entre les entrades x1, y1, x2, y2 i la sortida d és la fórmula de la distància euclidiana.

La solució ha de fer doncs tres tasques, l'una rera l'altra:

1. Llegir les coordenades x1, y1, x2, y2 dels dos punts. Aquestes coordenades han de ser nombres reals (amb decimals).

2. Calcular el valor de d a partir de x1, y1, x2, y2. Per a fer-ho, cal usar la fórmula de la distància euclidiana.

3. Escriure el valor de d.

En Python, això es pot fer codificar així:

x1 = float(input())
y1 = float(input())
x2 = float(input())
y2 = float(input())
d = ((x2 - x1)**2 + (y2 - y1)**2) ** 0.5
print(d)

Aquest cop, les quatre primeres línies assignen a les variables x1, y1, x2 i y2 els valors llegits de l'entrada. La cinquena línia assigna a d el valor pertinent a partir de x1, y1, x2 i y2 tot avaluant l'expressió ((x2 - x1)**2 + (y2 - y1)**2) ** 0.5. La sisena línia escriu el valor de d.

Recordeu que, en Python, l'operador ** és l'operador d'exponenciació. Per tant, x**2 és la mateixa cosa que $x^2$ i x**0.5 és la mateixa cosa que $\sqrt{x}$.

Jordi Petit
Lliçons.jutge.org
© Universitat Politècnica de Catalunya, 2026