Introducció als Mapes de Karnaugh

Un mapa de Karnaugh (també conegut com a K-map o diagrama de Veitch) és una eina gràfica utilitzada en electrònica digital per simplificar funcions lògiques booleanes de manera visual i sistemàtica.

L’objectiu principal és trobar l’expressió booleana més simple possible per a una funció lògica determinada. Una funció lògica més simple es tradueix directament en un circuit digital més senzill.

Es tracta d’un mètode alternatiu a la simplificació amb les lleis de l’àlgebra de Boole i és vàlid per a qualsevol nombre de variables. Resulta, però, més pràctic i intuïtiu per a poques variables, típicament de 2 a 4. Més enllà de 6 variables, els mapes de Karnaugh deixen de ser pràctics.

Un mapa de Karnaugh és una graella que organitza totes les combinacions possibles de les variables d’entrada d’una funció booleana. Cada cel·la representa una combinació de les variables d’entrada de la funció, és a dir, una fila de la taula de la veritat.

Aquest mapa s’ha d’ordenar de manera que entre dues cel·les adjacents verticalment o horitzontalment només canviï el valor d’una única variable. Això facilita la identificació de patrons i l’agrupació per reduir l’expressió lògica.

Exemple:

Vegem la següent taula de veritat d'un circuit digital hipotètic. Aquesta representa les variables d’entrada $A$, $B$ i $C$ i la sortida $S$.

Taula de veritat

A	B	C	S
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

El mapa de Karnaugh resultant, agrupant les variables B i C, és el següent:

	BC=00	BC=01	BC=11	BC=10
A=0	1	0	1	1
A=1	1	1	1	1

Els valors de cada cel·la són els valors que pren la sortida $S$ en funció de $A$, $B$ i $C$ en una fila de la taula.

Regles per al Mapa de Karnaugh

Codi Gray:

Les files i columnes del mapa no s'ordenen de manera convencional (00, 01, 10, 11), sinó que segueixen el codi Gray (00, 01, 11, 10). És a dir, entre dues cel·les adjacents (verticalment o horitzontalment) només canvia el valor d'una única variable.

Omplir la taula:

Cal omplir la taula amb els resultats de la variable de sortida corresponents a la combinació de valors d'entrada de cada cel·la.

Agrupar els $1$ adjacents:

L'objectiu és fer grups tan extensos com sigui possible.

• S'agrupen els $1$ adjacents en forma de fila, quadrat o rectangle.
• La mida dels grups ha de ser una potència de dos. És a dir 1, 2, 4, 8, etc.
• S'han d'anar fent grups fins que tots els $1$ de la taula formin part d'almenys un d'ells.
• Les vores del mapa es consideren adjacents amb la vora oposada, com si el mapa s'estengués repetint-se més enllà de les vores.

Obtenció de l'expressió lògica simplificada:

Cada grup de $1$ es tradueix en un terme de la funció booleana simplificada. Per fer-ho, s'observen quines variables no canvien de valor dins del grup; aquestes formaran part del terme de l'expressió. Les variables que canvien de valor dins del grup no apareixeran a l'expressió.

Estructures per a mapes de Karnaugh de 2 a 5 variables

A continuació es mostren les estructures dels mapes de Karnaugh per a diferents nombres de variables d'entrada. Les taules més comunes solen ser les de 2 a 4 variables d'entrada, però es poden utilitzar per a funcions de fins a 5 o 6 variables.

Mapa de Karnaugh de 2 variables d'entrada

A B	0	1
0
1

Mapa de Karnaugh de 3 variables d'entrada

En aquest cas, les variables es poden agrupar de diferents maneres; $A\mathrm{\setminus }BC$ (exemple anterior), $B\mathrm{\setminus }AC$ o $C\mathrm{\setminus }AB$ (aquest exemple). En qualsevol cas, el mapa de valors és el mateix (Codi Gray).

AB C	00	01	11	10
0
1

Mapa de Karnaugh de 4 variables d'entrada

El mapa de valors és invariable, l'agrupament de les variables $A$, $B$, $C$ i $D$ es pot fer com convingui en cada cas.

AB CD	00	01	11	10
00
01
11
10

Mapa de Karnaugh de 5 variables d'entrada

Fent servir el codi Gray el mapa de Karnaugh de 5 variables s'estructura de la manera següent:

ABC DE	000	001	011	010	110	111	101	100
00
01
11
10

Aquest mapa és utilitzable, però obvia que les columnes següents també es poden considerar adjacents.

• 000 amb 010
• 110 amb 100
• 001 amb 101
• 011 amb 111

Per aquesta raó, s’acostuma a representar amb una línia al centre que separa dos mapes 4×4 independents i que crea adjacències “creuades” entre els dos mapes, com si hi hagués un mirall vertical al centre. Aquest mapa es pot anomenar mapa de reflexió (reflection map).

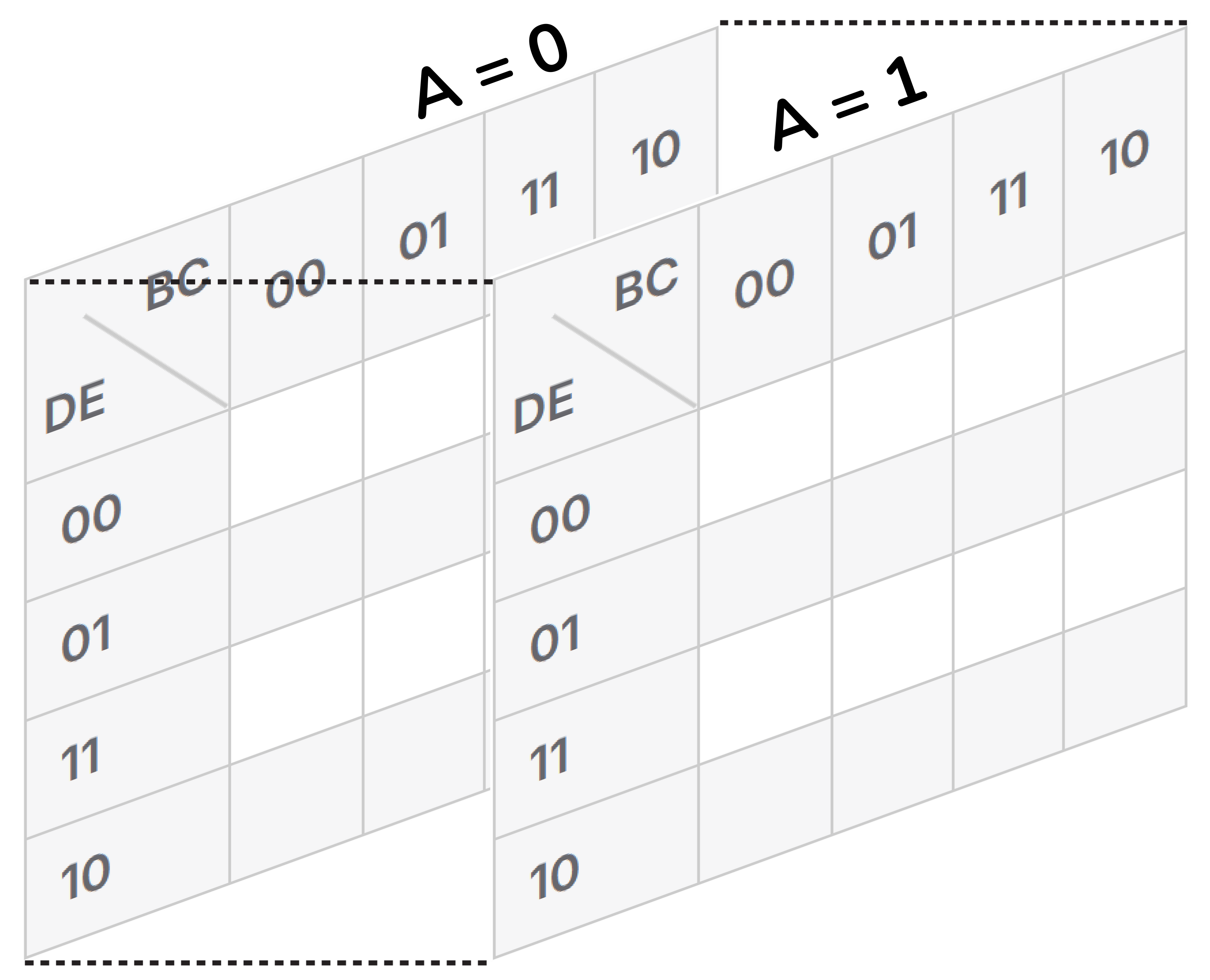
Una altra manera molt efectiva d'estructurar un mapa de Karnaugh de 5 variables és fer-ne dos de 4 variables: un d'ells representa $𝐴=0$ i l'altre $𝐴=1$, i considerant-los superposats en una tercera dimensió.

A=0 BC DE 00 01 11 10 00 01 11 10

A=1 BC DE 00 01 11 10 00 01 11 10

I visualitzar-los de la manera següent.

Exemple:

Busquem en el nostre exemple les agrupacions més extenses possibles de $1$. Hem de continuar amb el procés fins que tots els $1$ hagin estat considerats.

	BC=00	BC=01	BC=11	BC=10
A=0	1	0	1	1
A=1	1	1	1	1

En blau tenim quatre $1$ adjacents en forma de fila. La variable en comú en tots ells és $A=1$, les variables $B$ i $C$ canvien de valor. Així doncs, el primer terme de l'expressió de $S$ serà $A$.

$S=A+···$

	BC=00	BC=01	BC=11	BC=10
A=0	1	0	1	1
A=1	1	1	1	1

En groc tenim un grup de quatre $1$ adjacents en forma de quadrat. La variable en comú és $B=1$. Per tant el segon terme de l'expressió de $S$ és $B$.

$S=A+B+···$

	BC=00	BC=01	BC=11	BC=10
A=0	1	0	1	1
A=1	1	1	1	1

Encara ens queden $1$ per agrupar, així que en vermell tenim un altre grup de quatre $1$ adjacents en forma de quadrat. Aquest agrupament s'extén a través d'una vora de la taula. La variable que manté el seu valor és $C=0$, de manera que cal afegir el terme $C$ negat, $\overline{C}$.

$S=A+B+\overline{C}$

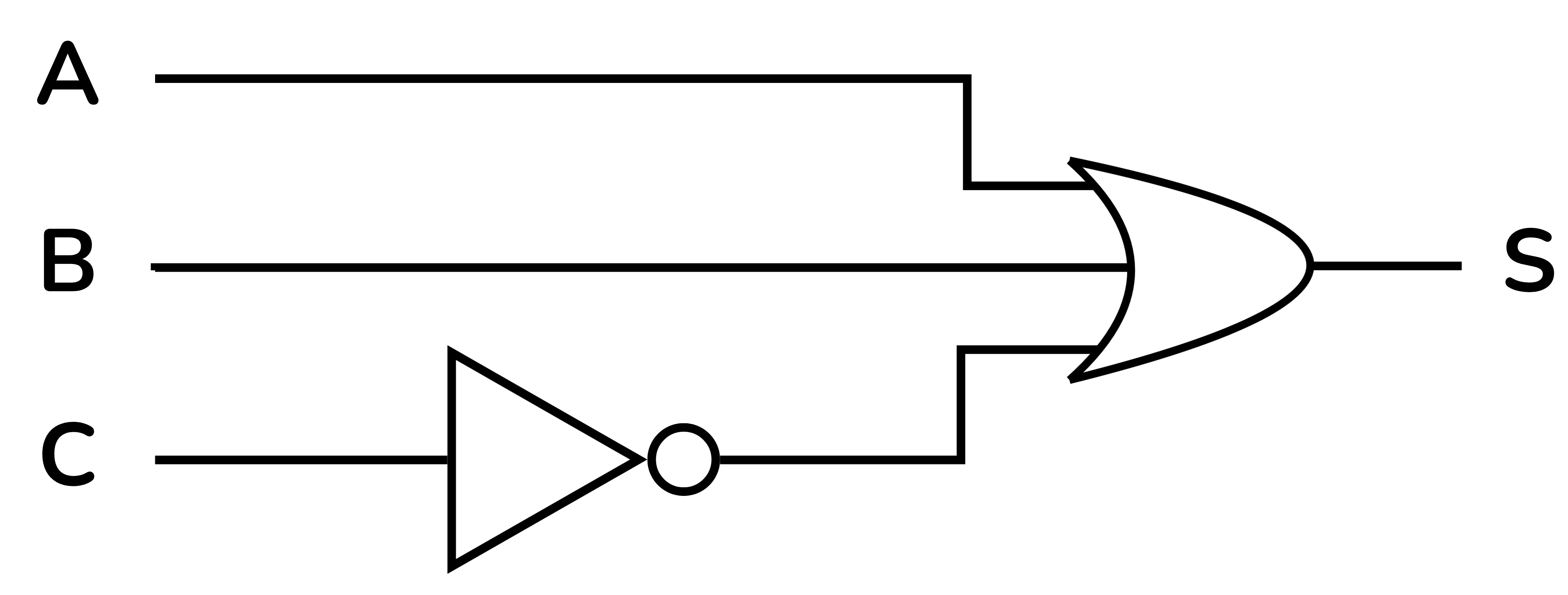
Aquesta és doncs l'expressió booleana simplificada que engendra la taula de veritat exemple. A partir d'aquesta es dedueix el circuit digital, tres entrades a una porta OR, una d'elles negada.

Altres exemples

Els següents exemples ens ajudaràn a entendre totes les regles.

Exemple:

AB C	00	01	11	10
0	1	1	0	0
1	0	0	1	1

El grup vermell engendra el terme $\overline{A}\overline{C}$ perque les variables constants són $A=0$ i $C=0$. Tant $A$ com $C$ han d'aparèixer negades perque tenen el valor $0$.

En el grup blau $A=1$ i $C=1$, per tant el seu terme a l'expressió booleana és $AC$.

L'expressió simplificada final és el següent.

$S=\overline{A}\overline{C}+AC$

El fet que no hi aparegui la variable $B$ significa que aquesta no té cap efecte en el resultat $S$.

Exemple:

AB C	00	01	11	10
0	1	0	0	1
1	0	0	0	0

Amb un sol grup en tenim prou en aquest exemple. Les variables constants són $B=0$ i $C=0$. L'expressió simplificada final té un sol terme.

$S=\overline{B}\overline{C}$

Exemple:

AB C	00	01	11	10
0	0	0	0	0
1	1	1	1	1

Altre cop, amb un sol grup en tenim prou. L'única variable que no canvia és $C=1$, d'aquesta manera $S$ només dependrà de $C$.

$S=C$

Exemple:

AB CD	00	01	11	10
00	1	0	0	1
01	0	1	1	0
11	0	1	1	0
10	1	0	0	1

En aquest exemple, el grup vermell agrupa $B=0$ i $D=0$, el grup blau agrupa $B=1$ i $D=1$.

$S=\overline{B}\overline{D}+BD$

Exemple:

AB C	00	01	11	10
0	0	1	1	1
1	1	0	1	1

Aquest exemple es pot solucionar amb tres grups. El vermell és $A$, el verd és $B\overline{C}$ i el blau $\overline{B}C$.

$S=A+B\overline{C}+\overline{B}C$

Xavier Casas, Francesc Madrid
Lliçons.jutge.org
© Universitat Politècnica de Catalunya, 2025