Comptadors

Els circuits seqüencials comptadors són circuits digitals capaços de passar per una seqüència ordenada d’estats en resposta a impulsos de rellotge. Cada estat representa un valor binari, i el circuit pot comptar cap endavant o cap enrere segons el disseny.

A diferència dels circuits combinacionals, l’estat actual d’un comptador depèn tant de les entrades com de l’estat anterior. Aquesta memòria s’implementa amb biestables, habitualment del tipus T, D o JK.

Els comptadors s’utilitzen en mesura de temps, generació de seqüències, divisió de freqüències i en blocs interns de rellotges digitals i processadors.

Els comptadors més comuns segueixen una seqüència binària: 0000, 0001, 0010, 0011, ..., i en arribar al valor màxim poden tornar a zero (comptador cíclic) o bé comptar enrere (bidireccional).

Comptador binari MOD $2^{n}$

Un comptador MOD $2^{n}$ és un circuit seqüencial amb $n$ biestables que compta de $0$ a $2^{n} - 1$ i després torna a zero. Té exactament $2^{n}$ estats diferents.

S’utilitza per comptar, generar seqüències i dividir freqüències.

Comptador d’un sol bit MOD $2^{1}$

El següent comptador té un sol bit, utilitza un sol biestable. És, per tant, un comptador MOD $2^{1}$ , i pot comptar de 0 a 1.

Aquest comptador utilitza un biestable D, un sumador complet (full adder) i un multiplexor. El sumador suma sempre $1$ al valor de $Q$ , de manera que el senyal $Q + 1$ arriba a l’entrada D del biestable.

El multiplexor serveix per afegir la possibilitat de reiniciar el comptador. El senyal selector actua doncs com un senyal de reinici (reset rst). Quan aquest senyal s’activa, el multiplexor connecta un valor constant $0$ al biestable, tot reiniciant el comptador.

Funcionament

Per entendre com funciona aquest comptador, comencem amb el biestable en un estat $Q = 0$ . La taula, més endavant, recull el resultat d’aquesta anàlisi.

Estat inicial:

El biestable es troba en un estat $Q = 0$ que passarà al sumador, que hi sumarà el valor $1$ .

Aquest senyal, amb valor $A + B = 1$ , retorna a l’entrada del biestable, l’entrada $D$ rep el senyal 1.

$D = 1$ però encara no s’ha actualitzat l’estat del biestable amb un senyal de rellotge, en conseqüència, $Q$ no canvia encara de valor.

El comptador és a zero ( $C o u n t = 0$ )

Primer pols:

Quan s’aplica un pols de rellotge el valor de $D$ es copia a la sortida $Q$ , que passa a tenir el valor $Q = 1$ .

El sumador hi suma el valor constant 1 i retornem al biestable el senyal $A + B = 0$ .

El bit de ròssec (carry) de sortida s'activa, $C_{s o r t i d a} = 1$ , però no el connectarem enlloc.

Ara l’entrada del biestable és $D = 0$ , però $Q$ no canvia encara de valor fins que no entri el següent pols de rellotge.

El comptador ha comptat fins a 1 ( $C o u n t = 1$ )

Segon pols: El següent pols de rellotge actualitza còpia el valor $D = 0$ a $Q$ , i així hem tornat a la situació inicial, on $C o u n t = 0$ .

Pols	$D$	$Q$	$C o u n t$
0	1	0	0
1	0	1	1
2	1	0	0
3	0	1	1

Podem visualitzar el funcionament d’aquest comptador amb el cronograma següent:

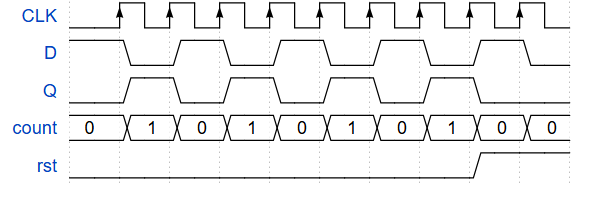
Sigui quin sigui l’estat del comptador, en el moment que activem el senyal de reinici ( $r s t$ ), el multiplexor forçarà el comptador a retornar al seu estat inicial.

Comptador de 3 bits MOD $2^{3}$

El següent comptador és de 3 bits, utilitza 3 biestables. És doncs un comptador MOD $2^{3}$ , capaç de comptar de $0$ a $7$ .

Aquest comptador es compon de 3 biestables D, 3 sumadors complets i, per tal d’afegir la possibilitat de reiniciar el comptador, 3 multiplexors.

Dels biestables n’obtindrem una sortida de 3 bits $Q = [Q_{2} Q_{1} Q_{0} ]$ . Les sortides $Q_{i}$ dels biestables es connecten als sumadors complets, que s’estructuren de manera equivalent al sumador de n bits. Per aquesta raó el bit de ròssec (carry) de cada sumador $C_{s o r t i d a}$ es connecta al bit de ròssec d’entrada $C_{e n t r a d a}$ del següent.

Aquest conjunt de 3 sumadors complets, és a dir, aquest sumador de 3 bits, afegirà contínuament la constant $B = 001$ a $Q$ . Per això connectem $B_{0} = 1$ , $B_{1} = 0$ i $B_{2} = 0$ .

El senyal de reinici (reset, o $r s t$ ) crearà un reinici síncron del comptador, retornant-lo a zero.

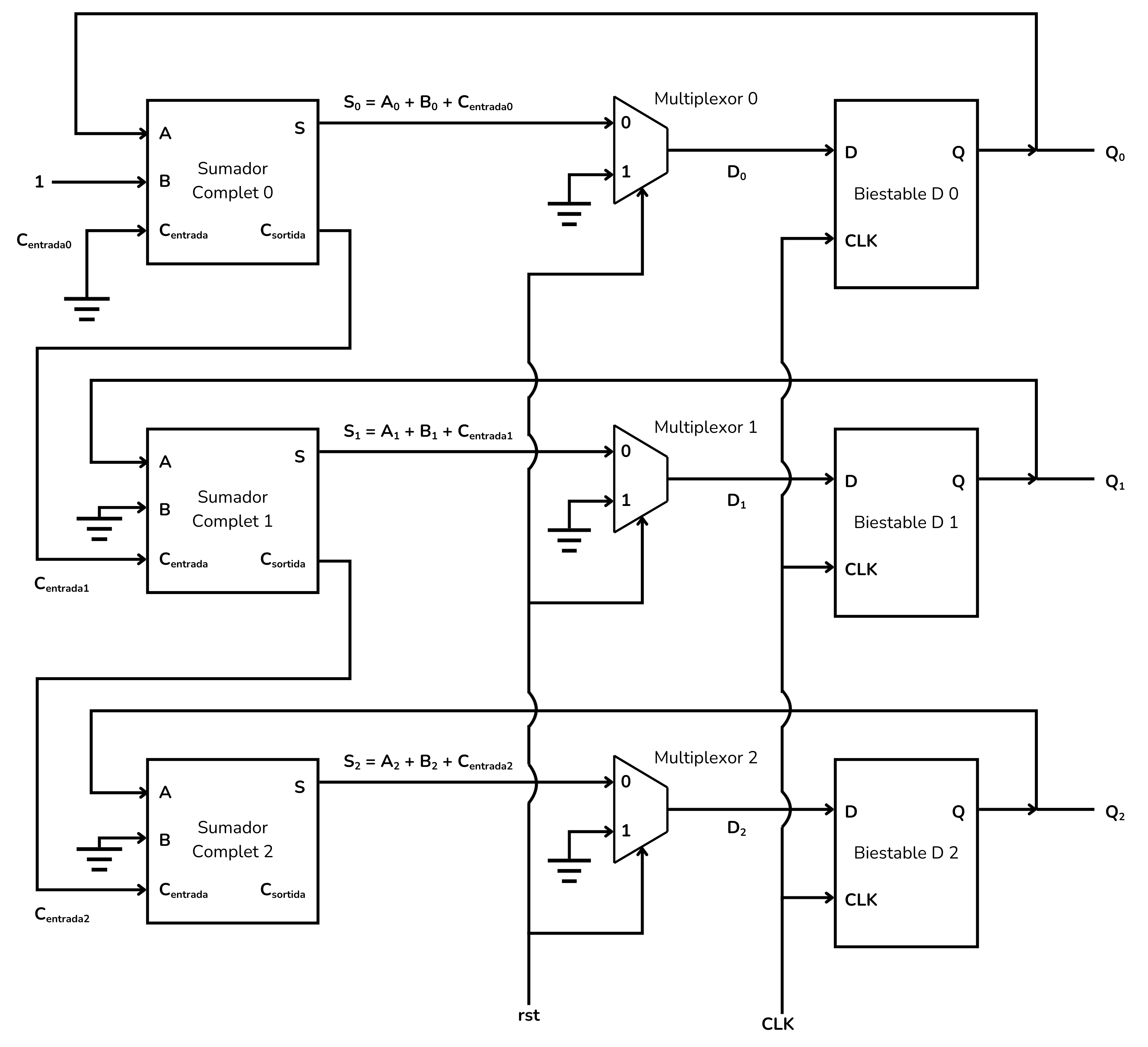
Funcionament

Analitzem el funcionament d’aquest comptador, començant amb tots els biestables a zero. La taula, més endavant, recull el resultat d’aquesta anàlisi.

Estat inicial:

Els biestables estan en l’estat $Q_{0} = 0$ , $Q_{1} = 0$ i $Q_{2} = 0$ .

El sumador 0 fa l'operació $0 + 1 + 0 = 1$ , per tant, $D_{0} = 1$ .

El sumador 1 fa l'operació $0 + 0 + 0 = 0$ , per tant, $D_{1} = 0$ .

El sumador 2 fa l'operació $0 + 0 + 0 = 0$ , per tant, $D_{2} = 0$ .

No hi ha cap bit de ròssec ( $C_{s o r t i d a}$ ) activat.

Primer pols:

El pols de rellotge fa que els bits de $Q$ s’actualitzin amb les entrades $D$ , de manera que $Q_{0} = 1$ , $Q_{1} = 0$ i $Q_{2} = 0$ .

Per tant, $D_{0} = 1$ , $D_{1} = 1$ i $D_{2} = 0$ , i $C_{s o r t i d a 0} = 1$

Segon pols:

El pols de rellotge fa que els bits de $Q$ s’actualitzin amb les entrades $D$ , de manera que $Q_{0} = 0$ , $Q_{1} = 1$ i $Q_{2} = 0$

Per tant, $D_{0} = 1$ , $D_{1} = 1$ i $D_{2} = 0$ , i no hi ha cap bit de ròssec activat.

Tercer pols:

El pols de rellotge fa que els bits de $Q$ s’actualitzin amb les entrades $D$ , de manera que $Q_{0} = 1$ , $Q_{1} = 1$ i $Q_{2} = 0$ .

Per tant, $D_{0} = 0$ , $D_{1} = 0$ i $D_{2} = 1$ .

Dos bits de ròssec de sortida estan activats, $C_{s o r t i d a 0} = 1$ i $C_{s o r t i d a 1} = 1$

Amb els següents polsos de rellotge, els biestables passen per totes les combinacions possibles, representant un nombre binari creixent fins a arribar al punt on tots els biestables són a l’estat 1. És a dir $Q = 111$ .

Setè pols:

Hem arribat al valor màxim del comptador, $Q_{0} = 1$ , $Q_{1} = 1$ i $Q_{2} = 1$ . El setè pols de rellotge durà el comptador altra vegada al seu estat inicial.

Pols	$D_{2}$	$D_{1}$	$D_{0}$	$C_{s o r t i d a 2}$	$C_{s o r t i d a 1}$	$C_{s o r t i d a 0}$	$Q_{2}$	$Q_{1}$	$Q_{0}$	$C o u n t$
0	0	0	1	0	0	0	0	0	0	000
1	0	1	0	0	0	1	0	0	1	001
2	0	1	1	0	0	0	0	1	0	010
3	1	0	0	0	1	1	0	1	1	011
4	1	0	1	0	0	0	1	0	0	100
5	1	1	0	0	0	1	1	0	1	101
6	1	1	1	0	0	0	1	1	0	110
7	0	0	0	1	1	1	1	1	1	111
8	0	0	1	0	0	0	0	0	0	000

Podem visualitzar el funcionament d’aquest comptador amb el cronograma següent:

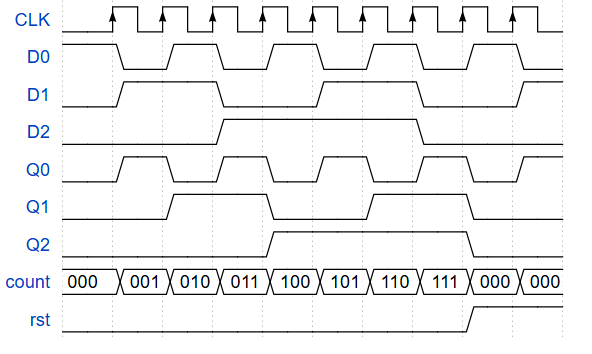
Sigui quin sigui l’estat del comptador, en el moment que activem el senyal de reinici (rst), el multiplexor forçarà el comptador a retornar al seu estat inicial.

Comptador de n bits MOD $2^{n}$

Per implementar un comptador de n bits cal encadenar n biestables, n sumadors i n multiplexors de la mateixa manera. Amb aquest comptador es pot comptar de 0 fins a $2^{n}$ .

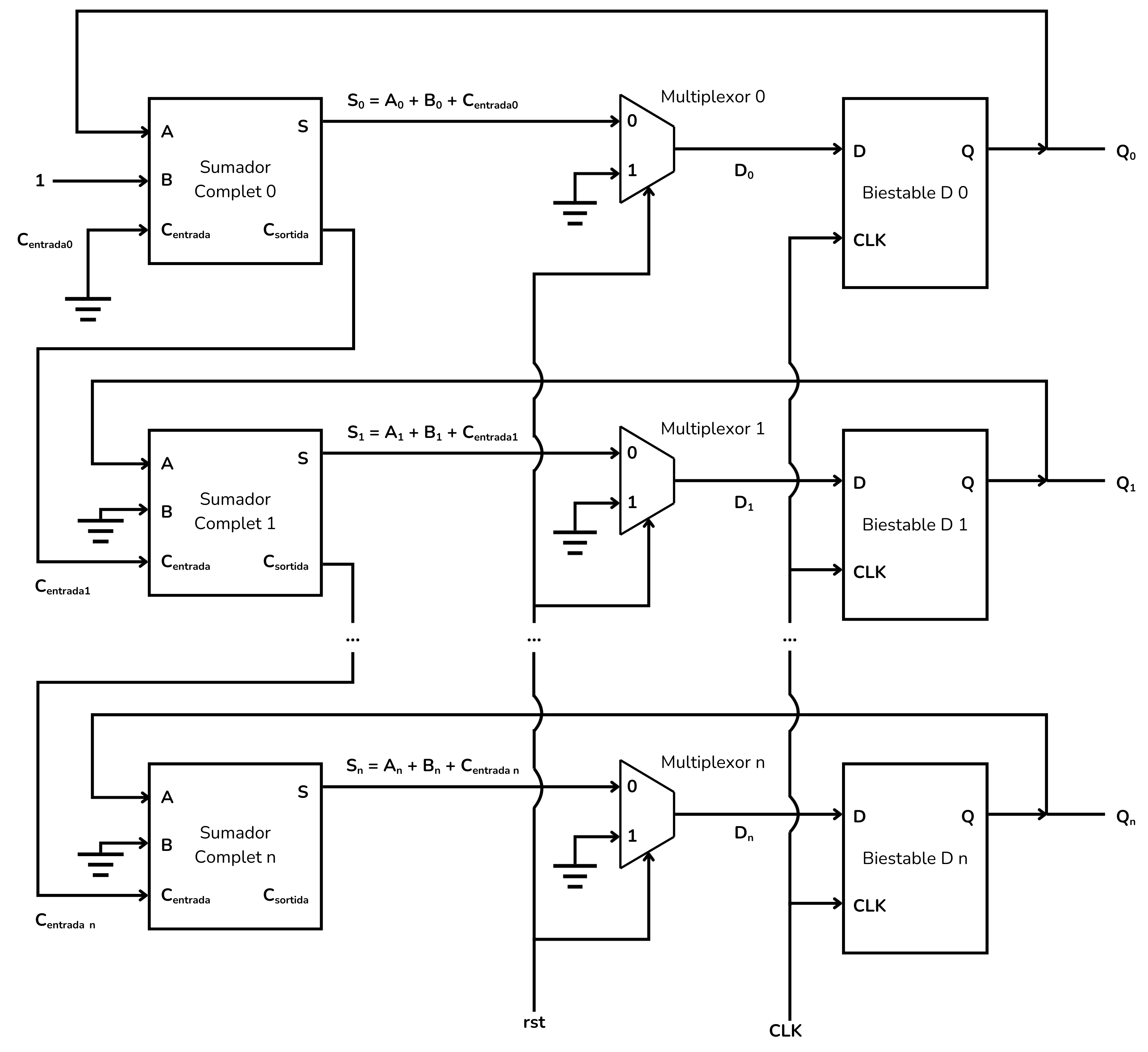
Comptador Binari Asíncron (Asynchronous Binary Counter o Ripple Counter):

Un comptador binari asíncron (Asynchronous Binary Counter), o comptador en cascada (Ripple Counter), s’implementa amb una sèrie de biestables, normalment del tipus JK. El primer biestable representa el bit menys significatiu LSB, que és controlat pel rellotge, i cadascun dels següents pel senyal de sortida de l’anterior, de manera que aquests biestables canvien d’estat en cascada.

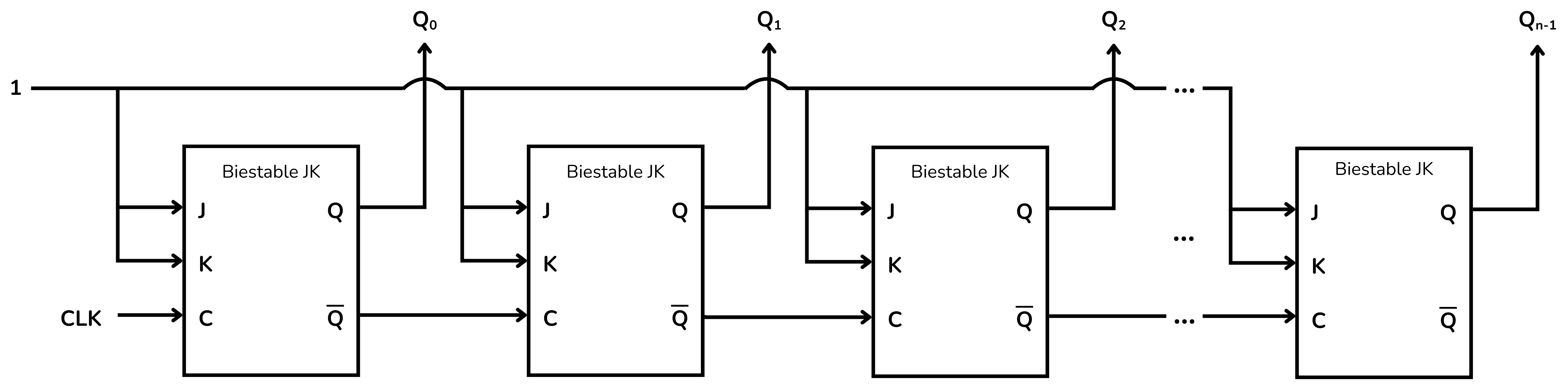
Els biestables JK estan connectats de manera que $J = K = 1$ i, per tant, l’estat de $Q$ es commuta entre 0 i 1 quan entra un senyal de rellotge.
Els biestables capten un senyal de rellotge només en el moment que aquest bit passa de 0 a 1. No es considerarà que entra senyal de rellotge mentres aquest es mantingui a 1, a 0 o commuti de 1 a 0.
La sortida $Q_{0}$ correspon al bit menys significatiu LSB la sortida $Q_{n}$ correspon al bit més significatiu MSB.
El senyal de rellotge extern s’aplica solament a l’entrada del primer biestable.
La sortida $\bar{Q}$ de cada biestable es connecta a l’entrada de rellotge del següent biestable.
- Això significa que quan un biestable commuti Q de 1 a 0, Q’ passarà de 0 a 1, estimulant l’entrada de rellotge del biestable següent. I això produirà una commutació de l’estat al biestable següent.
- Dit breument: un biestable commutarà d’estat només en el moment que el biestable anterior passa de 1 a 0.

Per entendre com funciona aquest comptador, comencem amb tots els biestables a ‘0’.

Primer pols:

El primer biestable $Q_{0}$ commuta de 0 a 1, $\bar{Q_{0}}$ passa de 1 a 0.

El segon biestable no detecta impuls a l’entrada de rellotge, no canvia d’estat i per tant $Q_{1}$ continua a 0.

El tercer biestable i tots els següents continuen a 0.

Segon pols:

El primer biestable $Q_{0}$ passa de 1 a 0, $\bar{Q_{0}}$ passa de 0 a 1.

El segon biestable detecta impuls a l’entrada de rellotge, $Q_{1}$ passa de 0 a 1 i $\bar{Q_{1}}$ passa de 1 a 0.

El tercer biestable i tots els següents continuen a 0.

Amb els següents polsos de rellotge. Les commutacions es van propagant de manera que els biestables passen per totes les combinacions possibles, representant un nombre binari creixent fins a arribar al punt on tots els biestables són a l’estat 1. En aquest punt, el següent pols de rellotge commuta el primer biestable de 1 a 0, el segon també, i així tots els biestables passen de 1 a 0 en cadena, tornant al punt de partida.

Aquesta taula mostra la seqüència dels diferents bits del comptador.

Pols	$Q_{3}$	$Q_{2}$	$Q_{1}$	$Q_{0}$	$C o u n t$
0	0	0	0	0	0000
1	0	0	0	1	1000
2	0	0	1	0	0100
3	0	0	1	1	1100
4	0	1	0	0	0010
···	···	···	···	···	···
14	1	1	1	0	0111
15	1	1	1	1	1111
16	0	0	0	0	0000

La figura següent mostra el cronograma d’aquest comptador.

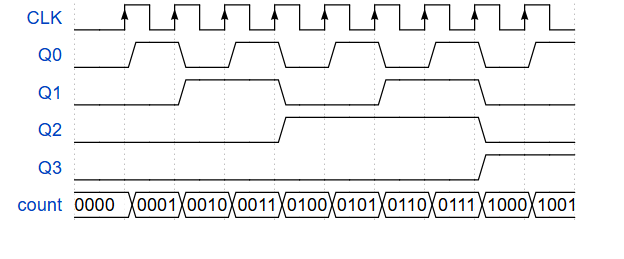
Aquest tipus de comptadors acumulen retards de tots els biestables a l’hora de passar d’un estat al següent, per tant, no és adequat per a freqüències de rellotge altes.

Els comptadors són també divisors de freqüència. Cada bit s’activa a la meitat de la freqüència del bit anterior de manera natural. És doncs un dispositiu que divideix successivament per 2 la freqüència de rellotge.

Comptador Binari Síncron (Synchronous Binary Counter):

Un comptador binari síncron és molt similar als comptadors asíncrons, però en aquest cas tots els biestables reben el mateix senyal de rellotge i canvien d'estat simultàniament.

Utilitza biestables de tipus JK i té la següent estructura:

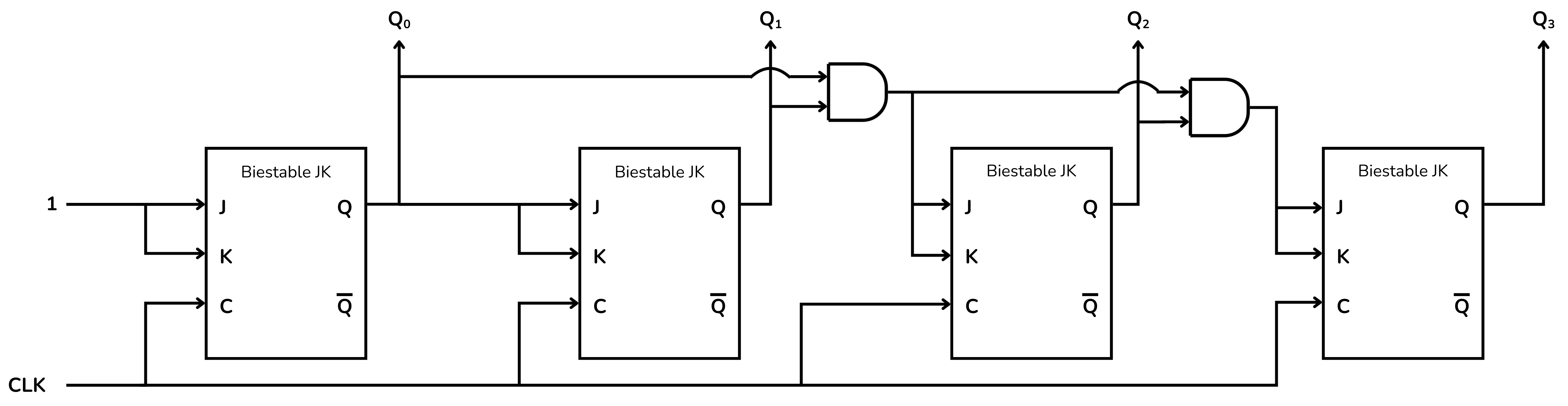
Al biestable 0 les entrades $J$ i $K$ estan connectades de manera que $J = K = 1$ i, per tant, la seva sortida $Q_{0}$ commuta entre 0 i 1 sempre que entri un senyal de rellotge $C L K$ .

La sortida del biestable 0 ( $Q_{0}$ ) està connectada directament a les entrades J i K del biestable 1. D’aquesta manera, quan $Q_{0} = 1$ , l’estat del biestable 1 ( $Q_{1}$ ) commutarà entre 0 i 1 sempre que entri un senyal de rellotge.

Les entrades $J$ i $K$ del biestable 2, i els següents biestables a partir d’aquest, estan controlades amb una porta $A N D$ , que rep les sortides dels dos biestables anteriors. Si les sortides dels dos biestables anteriors són iguals a 1 simultàniament, la porta $A N D$ s’activarà i les entrades del biestable rebran el senyal 1. En aquest cas, el biestable commutarà entre 0 i 1.

A partir del biestable 2, aquesta estructura es va repetint fins a completar el comptador.

Per entendre com funciona aquest comptador, comencem amb tots els biestables a ‘0’.

Estat inicial:

Tots els biestables estan a zero, $c o u n t = 0000$ .

Primer pols:

El primer biestable $Q_{0}$ commuta a $Q_{0} = 1$ . La resta de biestables no commuten perque les seves entrades són 0. En aquest pols el comptador ha passat a ser $c o u n t = 0001$ .

Segon pols:

Com que $Q_{0} = 1$ o $Q_{1} = 0$ el biestable 2 no commutarà. El biestable 1 commuta a 1 perque la seva entrada és 1. El biestable 0 commutarà a 0. En aquest pols el comptador ha passat a ser $c o u n t = 0010$ .

Tercer pols:

Com que $Q_{0} = 0$ i $Q_{1} = 1$ el biestable 2 no commutarà. El biestable 1 no commuta perque la seva entrada és 0. El biestable 0 commutarà a 1. En aquest pols el comptador ha passat a ser $c o u n t = 0011$ .

Quart pols:

Per primera vegada, la porta AND s’activa al rebre $Q_{0} = 1$ i $Q_{1} = 1$ , per tant el biestable 2 commuta a 1. El biestable 1 commuta a 0 perque la seva entrada és 1. El biestable 0 commutarà a 0. En aquest pols el comptador ha passat a ser $c o u n t = 0100$ .

Tant la taula, com el cronograma amb la seqüència del comptador són idèntiques al comoptador anterior.

Pols	$Q_{3}$	$Q_{2}$	$Q_{1}$	$Q_{0}$	$C o u n t$
0	0	0	0	0	0000
1	0	0	0	1	1000
2	0	0	1	0	0100
3	0	0	1	1	1100
4	0	1	0	0	0010
···	···	···	···	···	···
14	1	1	1	0	0111
15	1	1	1	1	1111
16	0	0	0	0	0000

Exemple: Comptador de 4 bits

En aquest exemple veurem com realitzar un comptador de 4 bits.

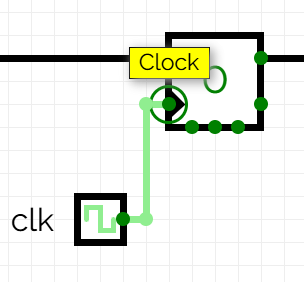
Les connexions del biestable que ens interessen són la D i Q, que marquen l'entrada i sortida de l'element de memòria, i també CLK, que és l’entrada del senyal de rellotge. L'entrada de rellotge representa sovint amb un triangle a l'interior de l'element.

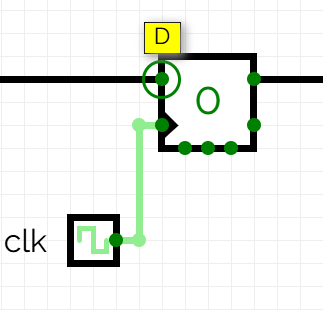
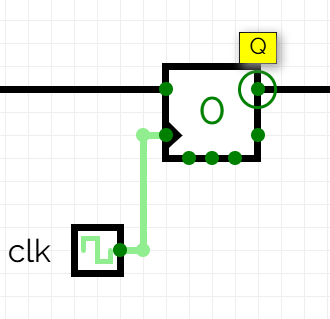
El biestable D també compta amb altres entrades com enables i resets que permeten reiniciar o eliminar estats d’informació. També té una sortida negada $\bar{Q}$ per si cal operar amb valors de sortida inversos.

Volem un comptador que segueixi una seqüència binària de 4 bits, de valors successius entre el 0000 i el 1111. També volem incloure un senyal de reset que retorni la sortida a 0000. Aquest comportament es pot aconseguir amb un sumador, un multiplexor i un biestable de 4 bits com a la figura.

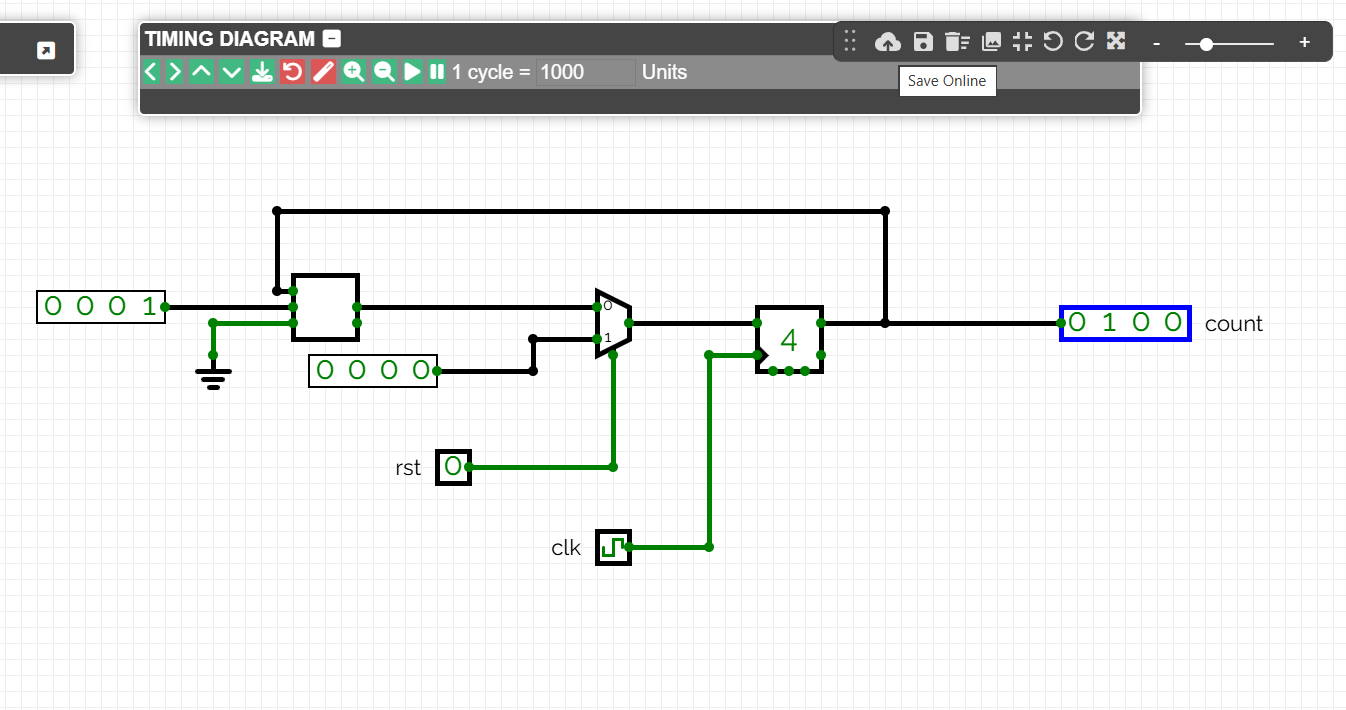
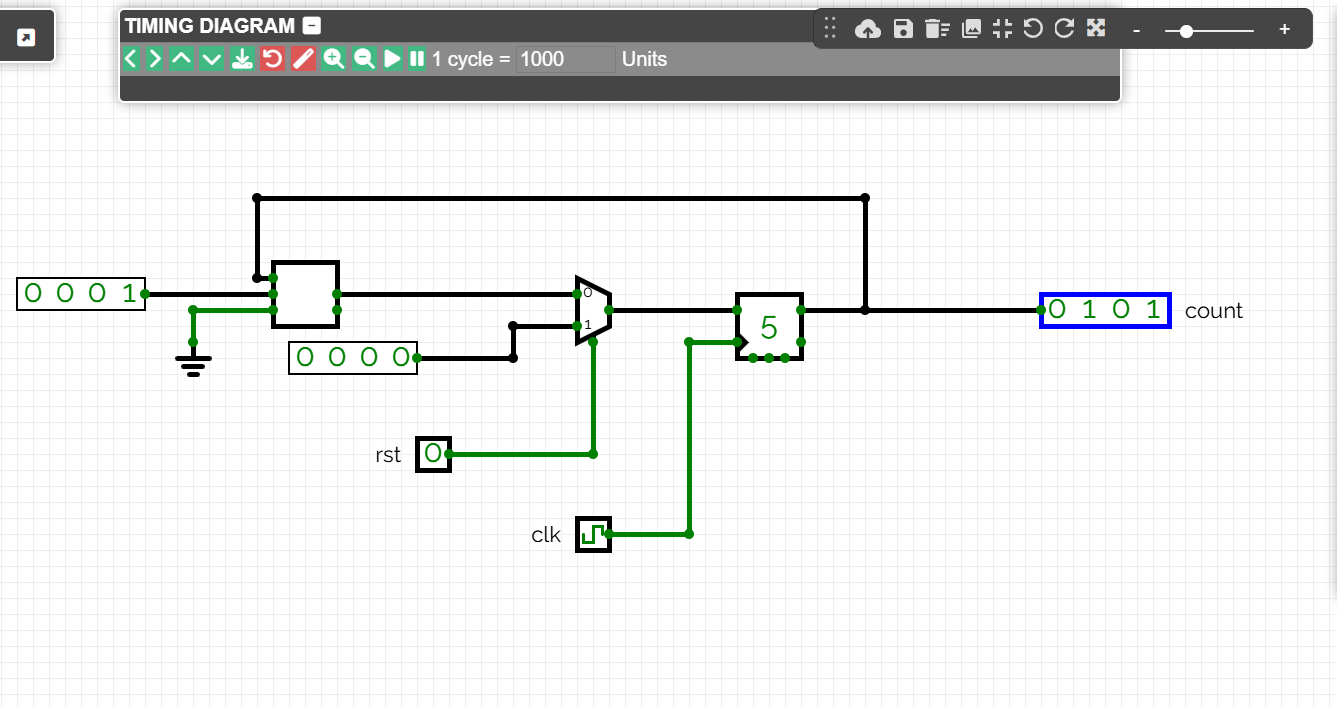
El pols de rellotge farà que el sumador afegeixi una constant 0001 al valor de sortida del biestable. En aquest exemple passant d'un valor 0100 a 0101.

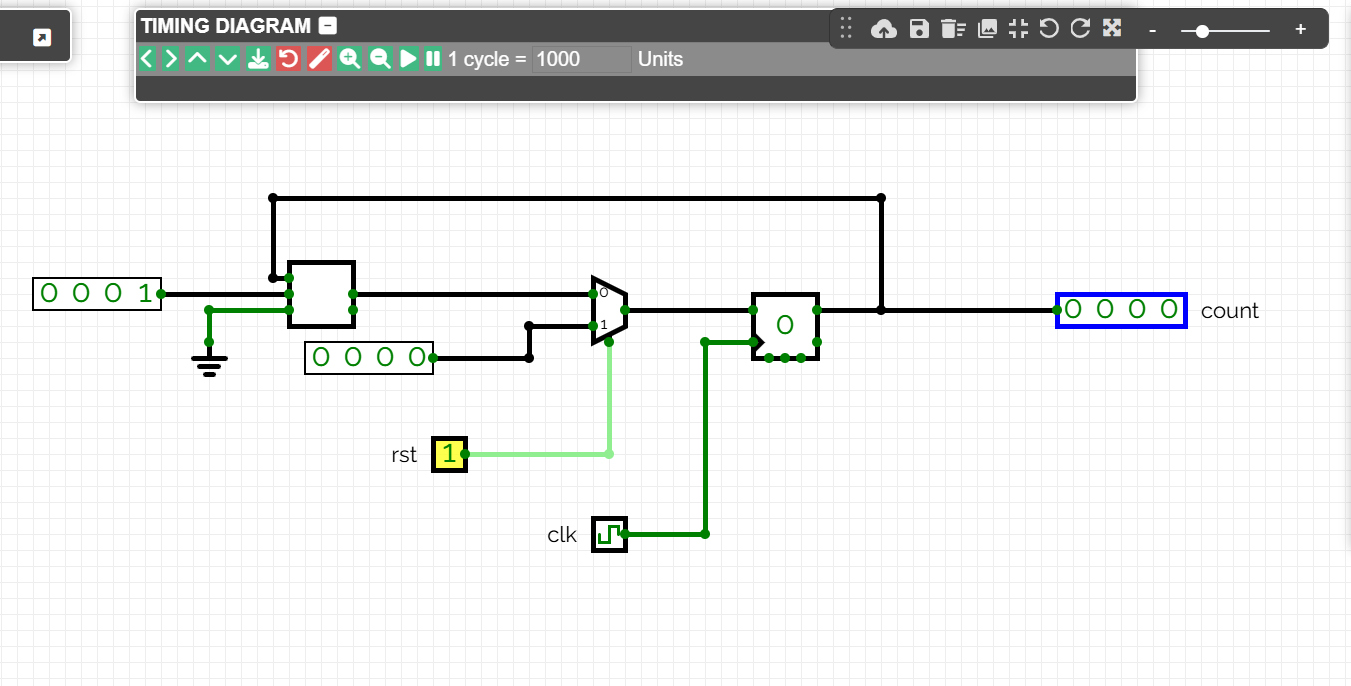
El multiplexor forçarà el reinici. Al entrar un senyal rst l'estat del biestable passarà a ser 0000.

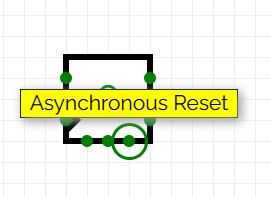
CircuitVerse inclou una entrada Asyncronous reset als biestables. Per fer un reinici asíncron cal eliminar el multiplexor i connectar el senyal $r s t$ a l'entrada Asyncronous reset del biestable.

Exercicis a Jutge.org: Introduction to Digital Circuit Design

Recorda que per accedir als exercicis i perquè el Jutge valori les teves solucions has d'estar inscrit al curs. Trobaràs totes les instruccions aquí.

Logos Càtedra Chip

Comptadors ​

Comptador binari MOD 2n ​

Comptador d’un sol bit MOD 21 ​

Funcionament ​

Comptador de 3 bits MOD 23 ​

Funcionament ​

Comptador de n bits MOD 2n ​

Comptador Binari Asíncron (Asynchronous Binary Counter o Ripple Counter): ​

Comptador Binari Síncron (Synchronous Binary Counter): ​

Exemple: Comptador de 4 bits ​

Exercicis a Jutge.org: Introduction to Digital Circuit Design ​

Comptadors

Comptador binari MOD $2^{n}$

Comptador d’un sol bit MOD $2^{1}$

Funcionament

Comptador de 3 bits MOD $2^{3}$

Funcionament

Comptador de n bits MOD $2^{n}$

Comptador Binari Asíncron (Asynchronous Binary Counter o Ripple Counter):

Comptador Binari Síncron (Synchronous Binary Counter):

Exemple: Comptador de 4 bits

Exercicis a Jutge.org: Introduction to Digital Circuit Design