Dígits BCD

En circuits digitals, un nombre Decimal Codificat en Binari (Binary Coded Decimal, BCD) és una manera de representar dígits decimals fent servir 4 bits. Cada dígit del 0 al 9 es converteix en una combinació binària fixa.

Dígit decimal	BCD
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001

Aquesta codificació és molt utilitzada en displays numèrics i calculadores.

Exemple: Disseny d’un circuit per a un display de 7 segments

Volem construir un circuit que rebi un dígit BCD i encengui els segments corresponents d’un display de 7 segments (de càtode comú) per mostrar-lo.

D [3 : 0] = [D_{3} D_{2} D_{1} D_{0}]

La figura següent mostra com s’anomenen els segments:

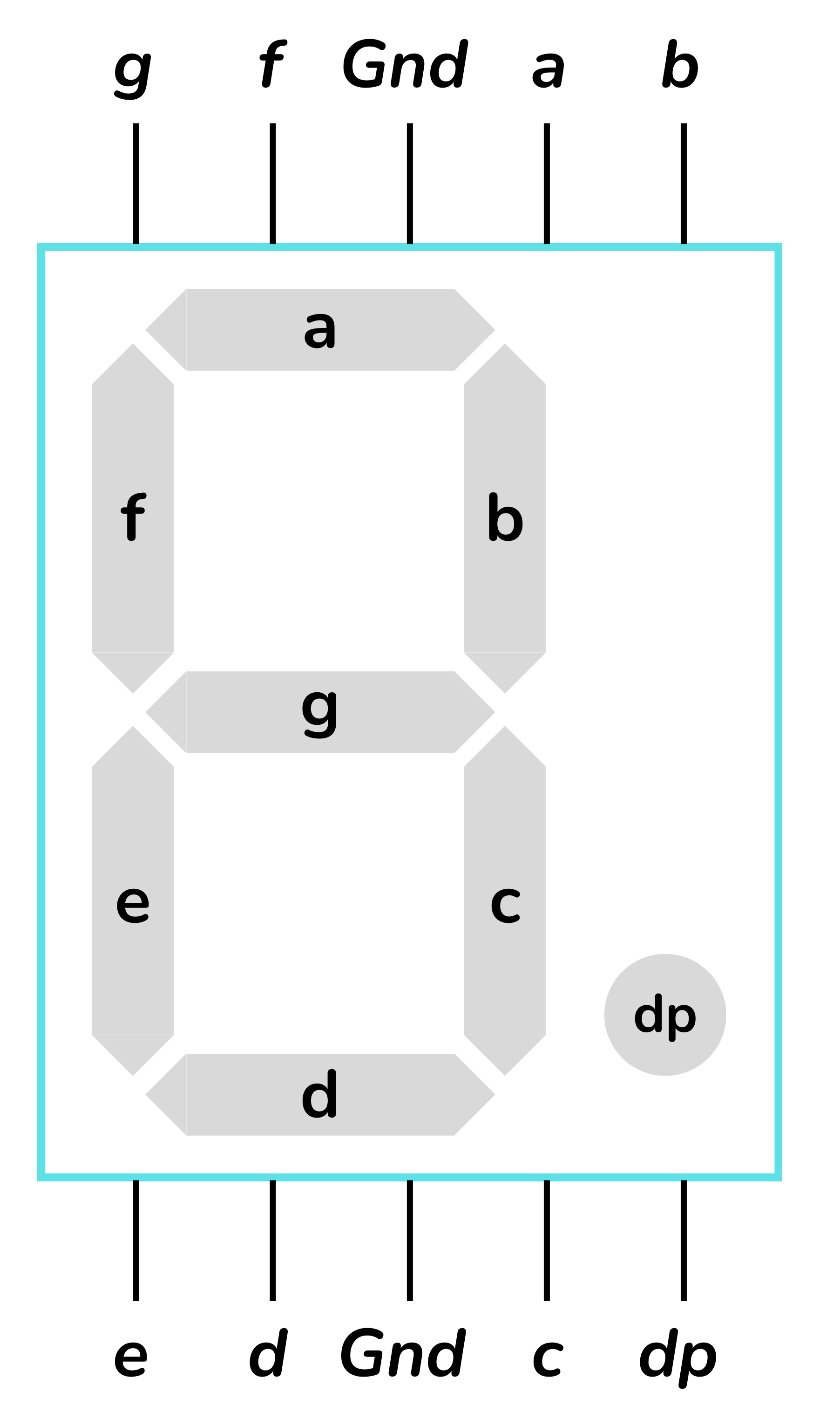
A la taula següent indiquem quins segments s’han d’encendre per a cada dígit decimal d'entrada $D [3 : 0]$ . Un 1 significa segment encès; un 0, apagat.

digit decimal	BCD $D_{3} D_{2} D_{1} D_{0}$	$a$	$b$	$c$	$d$	$e$	$f$	$g$
0	0000	1	1	1	1	1	1	0
1	0001	0	1	1	0	0	0	0
2	0010	1	1	0	1	1	0	1
3	0011	1	1	1	1	0	0	1
4	0100	0	1	1	0	0	1	1
5	0101	1	0	1	1	0	1	1
6	0110	1	0	1	1	1	1	1
7	0111	1	1	1	0	0	0	0
8	1000	1	1	1	1	1	1	1
9	1001	1	1	1	1	0	1	1
10 don't care	1010	x	x	x	x	x	x	x
11 don't care	1011	x	x	x	x	x	x	x
12 don't care	1100	x	x	x	x	x	x	x
13 don't care	1101	x	x	x	x	x	x	x
14 don't care	1110	x	x	x	x	x	x	x
15 don't care	1111	x	x	x	x	x	x	x

Condicions indiferents (don’t care)

Els 4 bits d’entrada poden codificar valors del 0 al 15. Però un dígit BCD només fa servir els valors del 0 al 9. Els casos del 10 al 15 no es mostraran mai i, per tant, els marquem com a x (don’t care).

A l’hora de buscar agrupacions al mapa de Karnaugh, els podem assignar els valors que més ens convinguin per tal obtenir expressions més simples.

Expressions booleanes simplificades

Cal fer un mapa de Karnaugh per a cadascuna de les sortides del circuit per tal d'obtenir l'expressió booleana per cada segment.

Pel que fa a les condicions indiferents, el valor de $x = 1$ dona com a resultat equacions més simples.

El procés complet i detallat es pot trobar a diverses fonts: enllaç 1, enllaç 2, enllaç 3

Obtenim les expressions següents per als segments:

Segment a:
$a = D_{3} + D_{1} + D_{2} \overset{―}{D_{0}} + \overset{―}{D_{2}} D_{0}$
Segment b:
$b = \overset{―}{D_{2}} + \overset{―}{D_{1}} \overset{―}{D_{0}} + D_{1} D_{0}$
Segment c:
$c = D_{2} + \overset{―}{D_{1}} + D_{0}$
Segment d:
$d = D_{3} + \overset{―}{D_{2}} \overset{―}{D_{0}} + D_{1} \overset{―}{D_{0}} + \overset{―}{D_{2}} \overset{―}{D_{1}} + D_{2} \overset{―}{D_{1}} D_{0}$
Segment e:
$e = \overset{―}{D_{2}} \overset{―}{D_{0}} + D_{1} \overset{―}{D_{0}}$
Segment f:
$f = D_{3} + D_{2} \overset{―}{D_{1}} + \overset{―}{D_{1}} \overset{―}{D_{0}} + D_{2} \overset{―}{D_{0}}$
Segment g:
$g = D_{3} + \overset{―}{D_{2}} D_{1} + D_{2} \overset{―}{D_{1}} + D_{1} \overset{―}{D_{0}}$

Aquestes expressions booleanes permeten implementar el circuit amb portes AND, OR i NOT. Les entrades són els bits $D_{3}, D_{2}, D_{1}, D_{0}$ i les sortides són els segments $a, b, c, d, e, f, g$ .

Aquest tipus de decodificador és molt habitual en electrònica digital bàsica.

Comprovació amb exemples

Per assegurar-nos que les fórmules funcionen correctament, calculem alguns dígits.

Exemple: dígit 2 $D = 0010$

Resultats esperats: segments a, b, d, e, g encès; c, f apagats.

$s e g m e n t a = 0 + 1 + 0 \cdot \bar{0} + \bar{0} \cdot 0 = 1$
$s e g m e n t b = \bar{0} + \bar{1} \cdot \bar{0} + 1 \cdot 0 = 1$
$s e g m e n t c = 0 + \bar{1} + 0 = 0$
$s e g m e n t d = 0 + \bar{0} \cdot \bar{0} + 1 \cdot \bar{0} + \bar{0} \cdot \bar{1} + 0 \cdot \bar{1} + 0 = 1$
$s e g m e n t e = \bar{0} \cdot \bar{0} + 1 \cdot \bar{0} = 1$
$s e g m e n t f = 0 + 0 \cdot \bar{1} + \bar{1} \cdot \bar{0} + 0 \cdot \bar{0} = 0$
$s e g m e n t g = 0 + \bar{0} \cdot 1 + 0 \cdot \bar{1} + 1 \cdot \bar{0} = 1$

Exemple: dígit 4 $(D = 0100$

Resultats esperats: segments b, c, f, g encès.

$s e g m e n t a = 0 + 0 + 1 \cdot \bar{0} + \bar{1} \cdot 0 = 1$
$s e g m e n t b = \bar{1} + \bar{0} \cdot \bar{0} + 0 \cdot 0 = 1$
$s e g m e n t c = 1 + \bar{0} + 0 = 1$
$s e g m e n t d = 0 + \bar{1} \cdot \bar{0} + 0 \cdot \bar{0} + \bar{1} \cdot \bar{0} + 1 \cdot \bar{0} \cdot 0 = 0$
$s e g m e n t e = \bar{1} \cdot \bar{0} + 0 \cdot \bar{0} = 0$
$s e g m e n t f = 0 + 1 \cdot \bar{0} + \bar{0} \cdot \bar{0} + 1 \cdot \bar{0} = 1$
$s e g m e n t g = 0 + \bar{1} \cdot 0 + 1 \cdot \bar{0} + 0 \cdot \bar{0} = 1$

Exemple: dígit 9 $D = 1001$

Resultats esperats: segments a, b, c, d, f, g encès.

$s e g m e n t a = 1 + 0 + 0 \cdot \bar{1} + \bar{0} \cdot 1 = 1$
$s e g m e n t b = \bar{0} + \bar{0} \cdot \bar{1} + 0 \cdot 1 = 1$
$s e g m e n t c = 0 + \bar{0} + 1 = 1$
$s e g m e n t d = 1 + \bar{0} \cdot \bar{1} + 0 \cdot \bar{1} + \bar{0} \cdot \bar{0} + 0 \cdot \bar{0} \cdot 1 = 1$
$s e g m e n t e = \bar{0} \cdot \bar{1} + 0 \cdot \bar{1} = 0$
$s e g m e n t f = 1 + 0 \cdot \bar{0} + \bar{0} \cdot \bar{1} + 0 \cdot \bar{1} = 1$
$s e g m e n t g = 1 + \bar{0} \cdot 0 + 0 \cdot \bar{0} + 0 \cdot \bar{1} = 1$

Exercicis a Jutge.org: Introduction to Digital Circuit Design

Recorda que per accedir als exercicis i perquè el Jutge valori les teves solucions has d'estar inscrit al curs. Trobaràs totes les instruccions aquí.

Logos Càtedra Chip

Dígits BCD ​

Exemple: Disseny d’un circuit per a un display de 7 segments ​

Condicions indiferents (don’t care) ​

Expressions booleanes simplificades ​

Comprovació amb exemples ​

Exemple: dígit 2 D=0010 ​

Exemple: dígit 4 (D=0100 ​

Exemple: dígit 9 D=1001 ​

Exercicis a Jutge.org: Introduction to Digital Circuit Design ​