Màquines d'estats

Una màquina d’estats (Finite State Machine, FSM) és un model matemàtic que descriu un sistema amb un nombre finit d’estats que canvia d’un estat a un altre en funció de l’estat actual, les entrades i unes regles determinades. Un circuit seqüencial pot implementar una FSM perquè té memòria i la seva sortida no depèn només de les entrades actuals.

Un circuit digital que implementa una màquina d’estats presenta aquestes característiques:

• Té un conjunt finit d’estats possibles, emmagatzemats en biestables.
• Té un conjunt de senyals d’entrada.
• Les transicions entre estats s’implementen amb lògica combinacional i depenen de l’estat actual i de les entrades.
• El senyal de rellotge coordina l’actualització de l’estat.

Hi ha dos models principals: màquina de Moore i màquina de Mealy.

Màquina de Moore

En una màquina de Moore la sortida depèn únicament de l’estat actual.

El comportament de les màquines d'estats es pot visualitzar amb un diagrama d’estats, que representa els estats de la màquina, les seves entrades i les seves sortides.

En el diagrama d’estats d’una màquina de Moore:

• Els estats s’indiquen amb cercles: E0, E1, E2…
• Les fletxes indiquen les transicions.
• Les entrades apareixen a les fletxes.
• La sortida s’indica dins del cercle (Estat/Sortida).

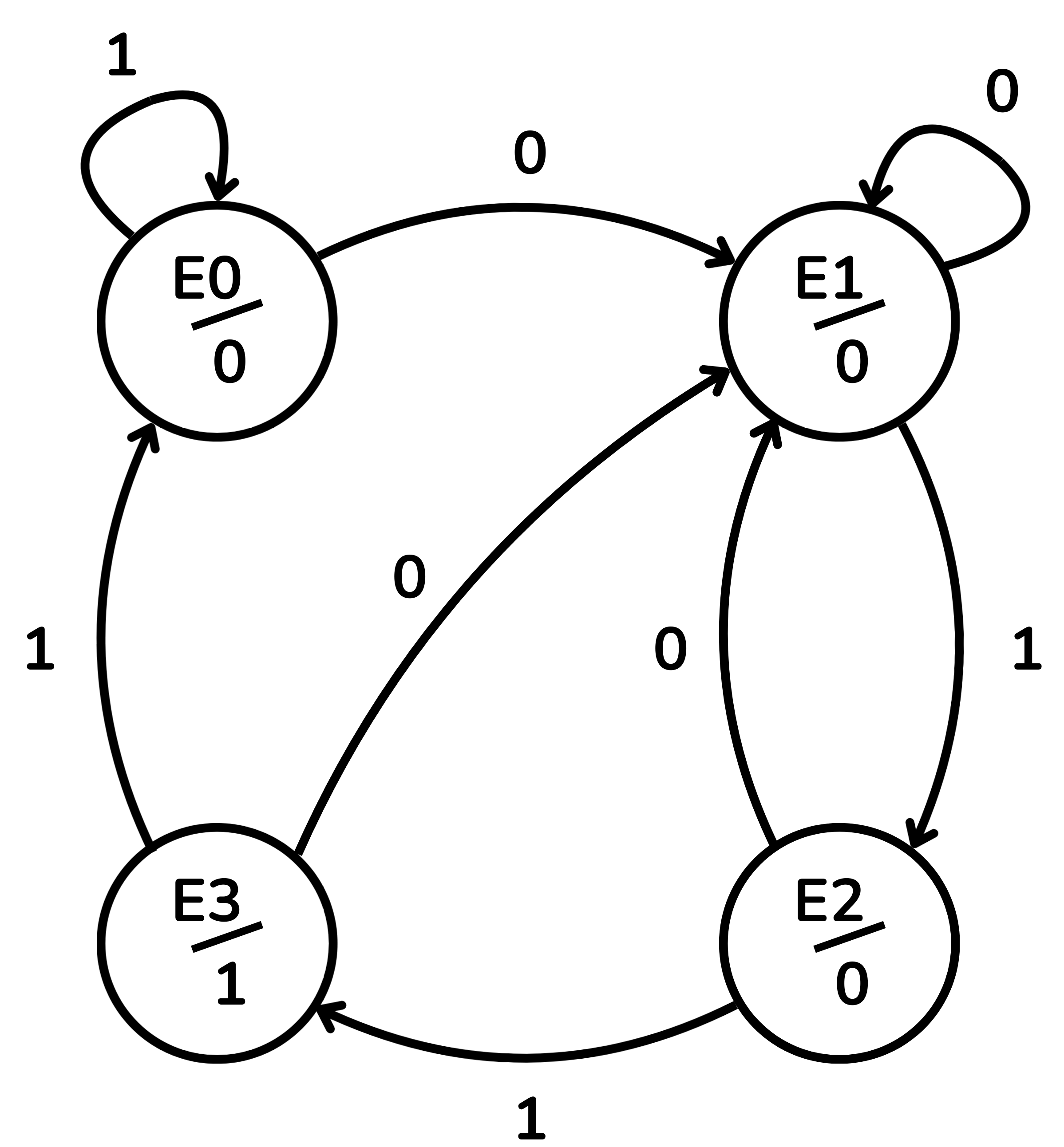
La taula següent ens ajudarà a navegar per aquest exemple de diagrama d’estats. La primera columna representa l’estat actual de la màquina i la seva sortida corresponent. Quan el senyal de rellotge provoca un canvi d’estat, l’estat següent dependrà de l’entrada. Si $Entrada=0$ la màquina canviarà a l’estat de la segona columna, si $Entrada=1$ canviarem a l’estat de la tercera columna.

Estat actual/Sortida	Estat següent
	Entrada=0	Entrada=1
E0 / 0	E1	E0
E1 / 0	E1	E2
E2 / 0	E1	E3
E3 / 1	E1	E0

Màquina de Mealy

En una màquina de Mealy, la sortida depèn de l’estat actual i de les entrades actuals. Quan la màquina és en cert estat, la sortida pot canviar si l'entrada canvia, sense esperar al següent canvi d’estat. Això pot generar impulsos transitoris entre canvis d’estat.

Avantatges:

• Sovint requereix menys estats que una màquina de Moore.
• Menys biestables i menys lògica combinacional.

En el diagrama d’estats:

• Els estats són cercles.
• Les fletxes indiquen transicions.
• Les etiquetes de fletxa mostren entrada/sortida.

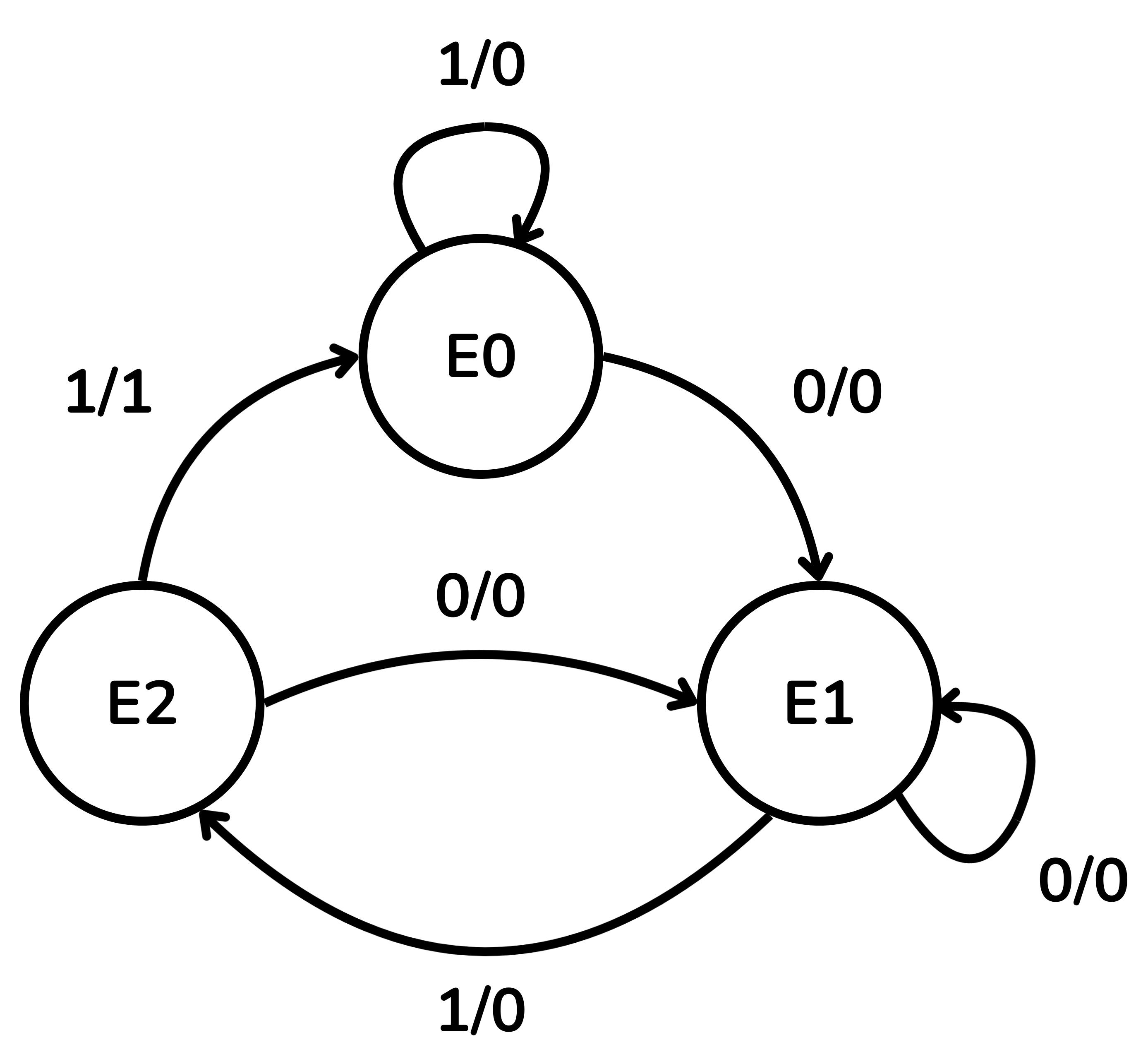
La taula a continuació ens ajudarà a entendre el diagrama d’estats. La primera columna representa l’estat actual de la màquina, la seva sortida també dependrà de l’entrada en aquell moment i es representa a les columnes segona i tercera. Només quan el senyal de rellotge ho indica, hi haurà un canvi, que ens durà a l’estat indicat a les columnes quarta i cinquena.

Estat actual	Sortida		Estat següent
	Entrada=0	Entrada=1	Entrada=0	Entrada=1
E0	0	0	E1	E0
E1	0	0	E1	E2
E2	0	1	E1	E0

Les màquines d'estats són fonamentals per dissenyar components lògics que necessiten seguir una seqüència o un protocol. S'utilitzen en:

• controladors de protocols digitals (SPI, I2C, UART),
• seqüenciadors d’operacions complexes (unitats de control),
• detectors de patrons o seqüències,
• semàfors digitals o sistemes de control.

Exemple: Retardador (delay line) de 2 cicles

Aquest circuit llegeix una seqüència binària i la replica amb un retard de dos cicles. Durant els dos primers cicles, la sortida val 0.

Prenem per exempla la següent seqüència inicial de nombres:

$S_{entrada}:1,1,0,0,1,1,1,1,0,0,0,1,0,1,\dots$

Seqüència de sortida (retardada 2 cicles):

$S_{sortida}:0,0,1,1,0,0,1,1,1,1,0,0,0,1,0,1,\dots$

Per causar el retard utilitzem dos biestables D en sèrie:

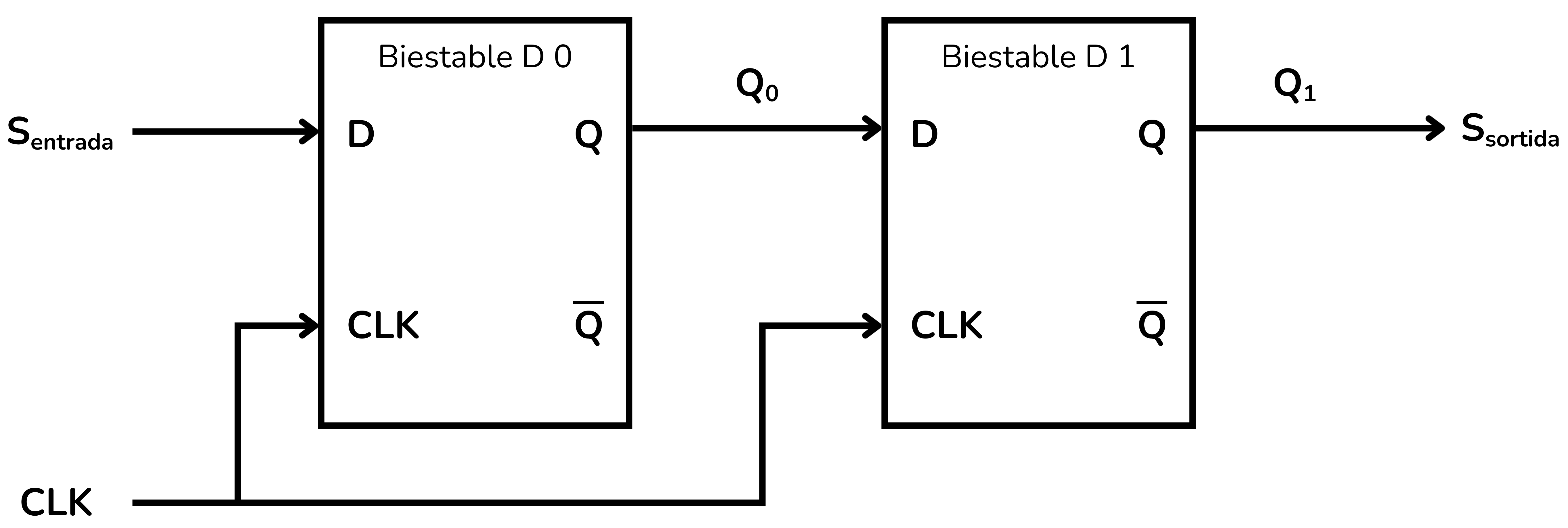
A cada pols de rellotge passarà el següent:

• El valor que tenia el biestable 1 és llegit com a sortida $S_{sortida}$.
• El valor que tenia el biestable 0 ($Q_0$) passa al biestable 1 ($Q_1$).
• L’entrada $S_{entrada}$ es copia al Biestable 0.

Aquesta estructura retarda qualsevol entrada dos cicles.

Al fer servir dos biestables D la màquina té $2^2$ combinacions diferents, és a dir, 4 estats possibles que anomenarem $E0$,$E1$,$E2$ i $E3$:

Estat	[$Q_1$, $Q_0$]
E0	00	Estat inicial (Buit)
E1	01	L’últim bit que ha entrat a $Q_0$ és 1 el bit més antic $Q_1$ és 0
E2	10	L’últim bit que ha entrat a $Q_0$ és 0 el bit més antic $Q_1$ és 1
E3	11	Els dos darrers bits que han entrat són 1

La taula a continuació especifica els canvis d’estat possibles segons l’entrada $S_{entrada}$.

Estat actual	Estat Següent
	Sentrada=0	Sentrada=1
00 (E0)	00 (E0)	01 (E1)
01 (E1)	10 (E2)	11 (E3)
10 (E2)	00 (E0)	01 (E1)
11 (E3)	10 (E2)	11 (E3)

A aquest circuit li afegirem un senyal de reinici $rst$ (reset) que retorni tots els biestables a 0. Si $rst=1$, els dos biestables es reinicien i tornem a l’estat inicial E0. Si $rst=0$, el circuit continua funcionant amb normalitat.

El diagrama d’estats complet és:

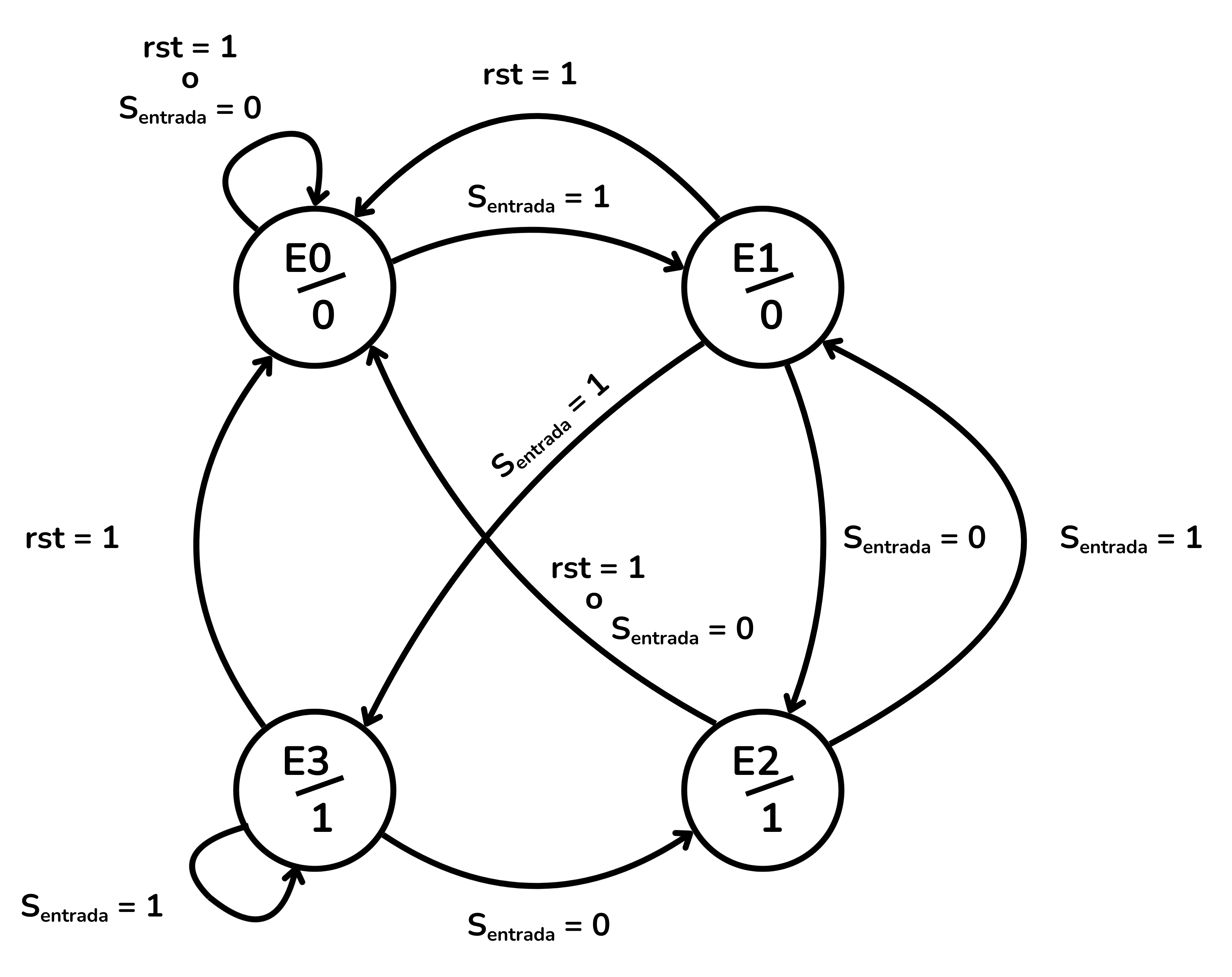
Com que la sortida $S_{sortida}$ depèn únicament de l’estat actual, aquest circuit és una màquina de Moore.

Una vegada fet el diagrama d’estats, passem a muntar el circuit a CircuitVerse. Muntem els dos biestables D en sèrie compartint el mateix senyal de rellotge i el mateix senyal de reinici (rst).

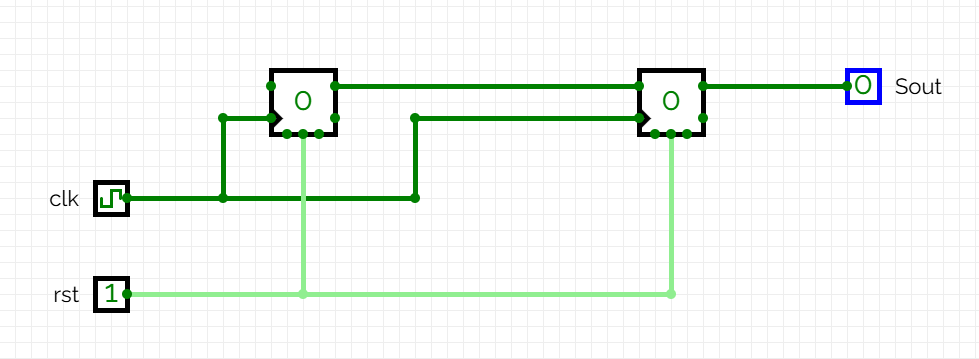
En els exercicis de Jutge els senyals de reinici són sempre síncrons, per tant, així ho farem en aquest exemple, connectant els dos biestables al mateix reset síncron.

Cal connectar doncs el senyal rst a l’entrada Preset del biestable D i no a l'entrada Asynchronous reset (reinici asíncron).

Per inicialitzar els valors, afegim dos multiplexors. El senyal rst és el selector:

• El primer multiplexor tindrà com a entrades el senyal d’entrada $S_{entrada}$ i una constant 0. La seva sortida estarà connectada a l’entrada $D$ del primer biestable.
• El segon multiplexor tindrà com a entrades la sortida $Q$ del primer biestable i la mateixa constant 0. La seva sortida estarà connectada a l’entrada $D$ del segon biestable.

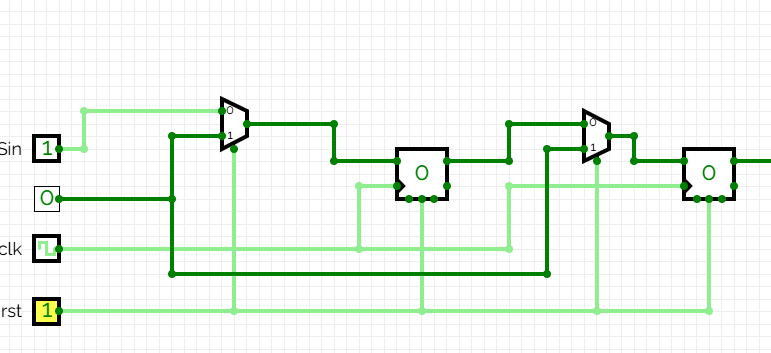
Comprovarem el seu funcionament amb una seqüència inicial d'exemple:

$S_{entrada}:1,1,1,\dots$

Amb rst = 1, els biestables són a 0 (estat E0) i $S_{sortida}=0$.

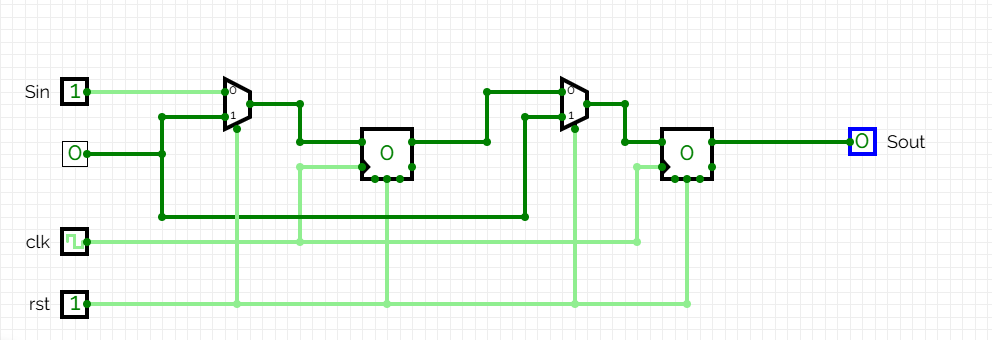
Amb rst=0, deixem evolucionar el circuit.

En el primer flanc de rellotge el valor de $S_{entrada}=1$ es carrega al primer biestable. L’estat 0 del primer biestable passa al segon biestable i $S_{sortida}$ continua tenint un valor de 0. Hem passat doncs a l'estat $E1$.

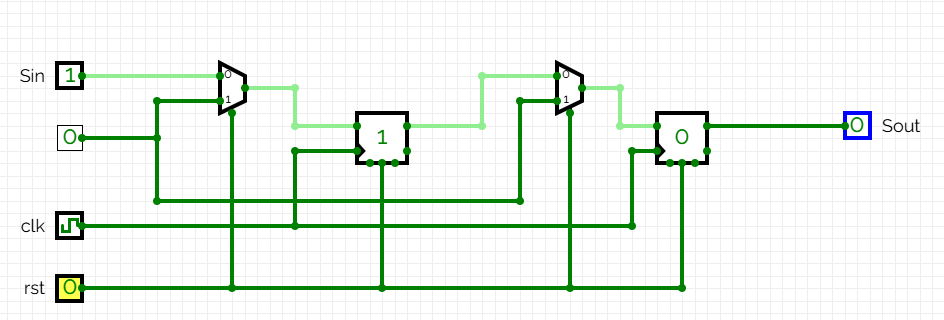
En el segon flanc de rellotge, el valor de $S_{entrada}=1$ es carrega al primer biestable, el valor del primer biestable 1 es carrega al segon biestable i per tant $S_{sortida}=1$. Ens trobem a l'estat $E2$.

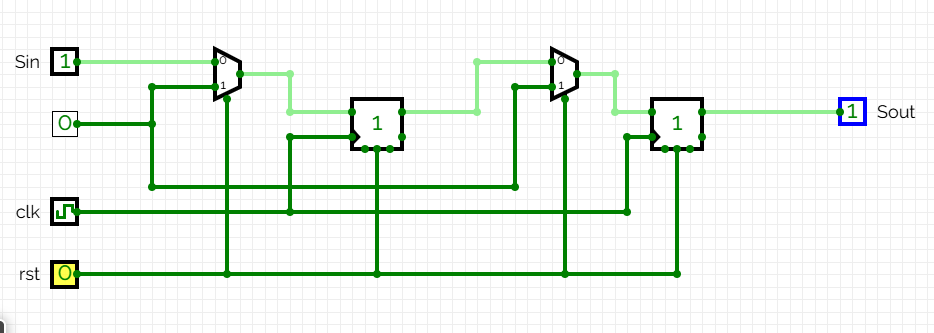
En aquest punt del procés, el primer valor de $S_{entrada}$ s'ha traslladat des de l'entrada fins a la sortida passant pels dos biestables. Els dos valors següents estan carregats als biestables i els senyals de rellotge successius els aniràn traslladant cap a la sortida. Aquest circuit implementa doncs una cua entre $S_{entrada}$ i $S_{sortida}$ que el senyal d'entrada triga dos cicles en travessar.

En aquests dos primers senyals de rellotge, les seqüències d'entrada i de sortida han implementat efectivament un retard de dos cicles:

$S_{entrada}$ : 1, 1, 1, …

$S_{sortida}$ : 0, 0, 1, …

Exercicis a Jutge.org: Introduction to Digital Circuit Design

• Last two equal
• Delayed sequence
• Even number of 0's and 1's
• Circuit from state diagram
• Sequence 110
• Recognizing sequences
• Is it divisible by 3?
• Simple state machine
• Traffic-light controller
• Vending machine

Recorda que per accedir als exercicis i perquè el Jutge valori les teves solucions has d'estar inscrit al curs. Trobaràs totes les instruccions aquí.

Xavier Casas, Francesc Madrid
Lliçons.jutge.org
© Universitat Politècnica de Catalunya, 2025