

Nombres
En els circuits digitals, els nombres s’implementen en notació binària i totes les operacions matemàtiques -suma, resta, comparació, multiplicació, divisió o mòdul- es realitzen manipulant bits.
Exemple: Nombre parell o senar
Dissenyarem un circuit que rebi a l’entrada un nombre de 4 bits i activi la sortida (
Un nombre binari és parell si el seu bit menys significatiu (LSB) val
Definim la variable d’entrada:
El bit menys significatiu és
La sortida és un sol bit:
si el nombre és parell. si el nombre és senar.
Taula parcial d’exemples (la completa tindria 16 files):
| Nombre en decimal | Paritat | |||
|---|---|---|---|---|
| 0000 | 0 | 0 | Parell | 1 |
| 0001 | 1 | 1 | Senar | 0 |
| 0010 | 2 | 0 | Parell | 1 |
| 0011 | 3 | 1 | Senar | 0 |
| 1110 | 14 | 0 | Parell | 1 |
| 1111 | 15 | 1 | Senar | 0 |
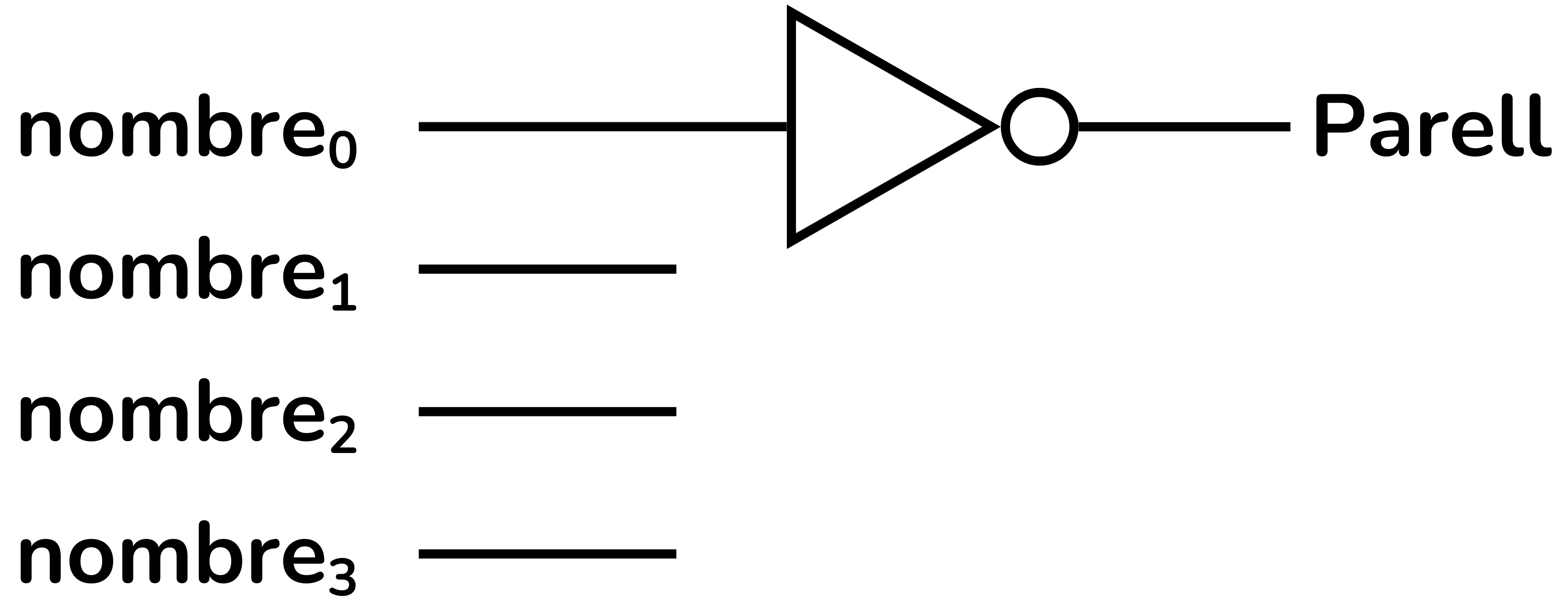
Construir el circuit és força directe, la sortida
La sortida és doncs la negació de
Per tant, només cal una porta NOT.
Exemple: Mòdul 7 d’un nombre de 4 bits
Dissenyarem un circuit que calculi el mòdul 7 d’un número binari
Un número de 4 bits
Els residus després de dividir un nombre per 7 poden prendre valors de 0 a 6. Per tal de representar el resultat de l'operació, n’hi haurà prou amb un nombre de 3 bits, que pot prendre valors del 000 al 111 (del 0 al 7 en decimal).
El primer pas per dissenyar aquest circuit és crear la taula de veritat completa que relaciona cada entrada n de 4 bits
| 0 | 0000 | 0 | 000 |
| 1 | 0001 | 1 | 001 |
| 2 | 0010 | 2 | 010 |
| 3 | 0011 | 3 | 011 |
| 4 | 0100 | 4 | 100 |
| 5 | 0101 | 5 | 101 |
| 6 | 0110 | 6 | 110 |
| 7 | 0111 | 0 | 000 |
| 8 | 1000 | 1 | 001 |
| 9 | 1001 | 2 | 010 |
| 10 | 1010 | 3 | 011 |
| 11 | 1011 | 4 | 100 |
| 12 | 1100 | 5 | 101 |
| 13 | 1101 | 6 | 110 |
| 14 | 1110 | 0 | 000 |
| 15 | 1111 | 1 | 001 |
Per a cada sortida (
Sortida
Muntem el mapa de Karnaugh de 4 variables d'entrada per a la sortida
n1 n0 n3 n2 | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 0 | 1 | 1 | 0 |
| 01 | 0 | 1 | 1 | 0 |
| 11 | 0 | 1 | 0 | 0 |
| 10 | 0 | 1 | 1 | 0 |
n1 n0 n3 n2 | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 0 | 1 | 1 | 0 |
| 01 | 0 | 1 | 1 | 0 |
| 11 | 0 | 1 | 0 | 0 |
| 10 | 0 | 1 | 1 | 0 |
n1 n0 n3 n2 | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 0 | 1 | 1 | 0 |
| 01 | 0 | 1 | 1 | 0 |
| 11 | 0 | 1 | 0 | 0 |
| 10 | 0 | 1 | 1 | 0 |
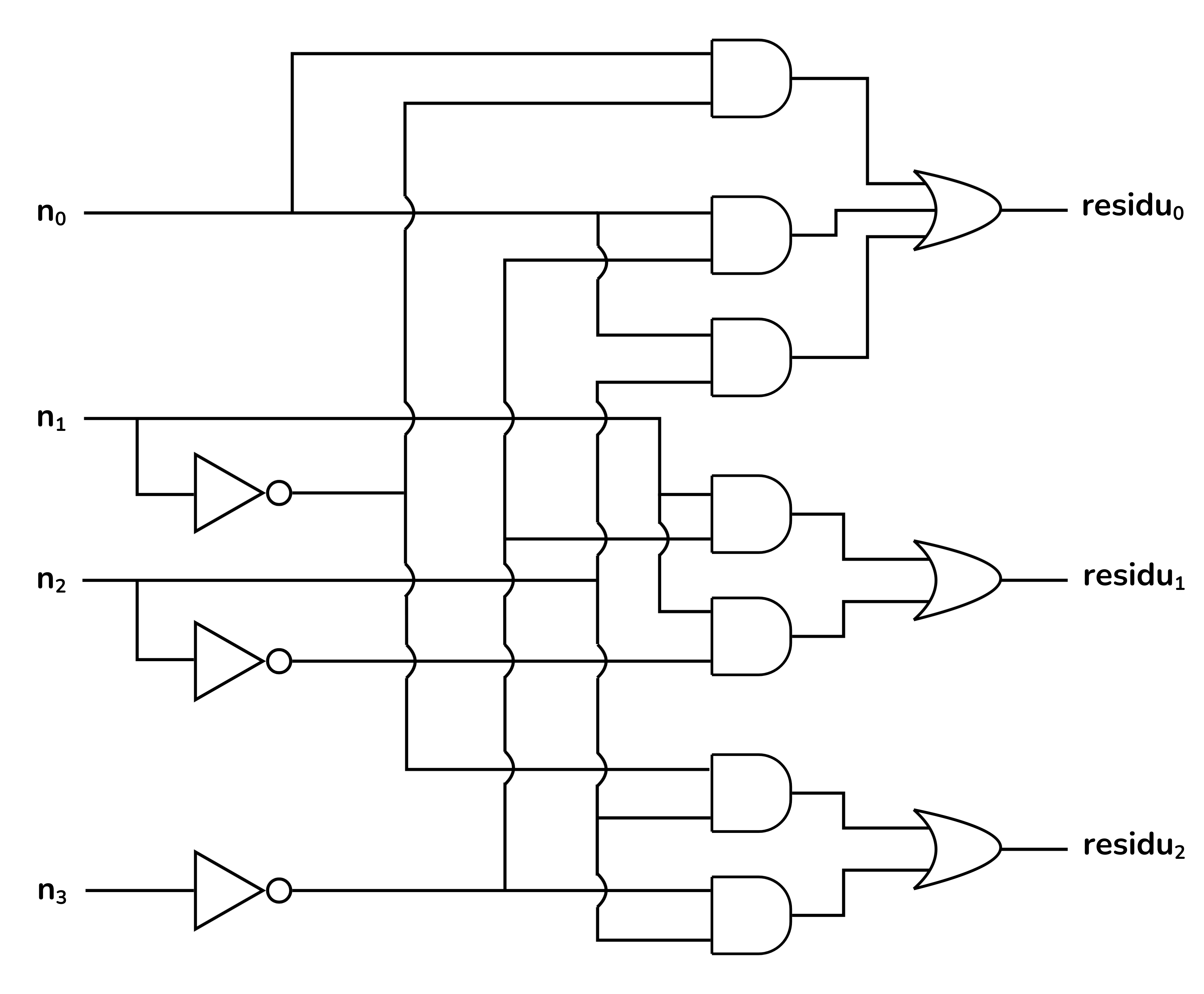
L'expressió booleana simplificada per a
Sortida
Muntem el mapa de Karnaugh de 4 variables d'entrada per a la sortida
n1 n0 n3 n2 | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 0 | 0 | 1 | 1 |
| 01 | 0 | 0 | 1 | 1 |
| 11 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 1 | 1 |
n1 n0 n3 n2 | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 0 | 0 | 1 | 1 |
| 01 | 0 | 0 | 1 | 1 |
| 11 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 1 | 1 |
L'expressió booleana simplificada per a
Sortida
Per a la sortida
n1 n0 n3 n2 | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 0 | 0 | 0 | 0 |
| 01 | 1 | 1 | 1 | 1 |
| 11 | 1 | 1 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 |
n1 n0 n3 n2 | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 0 | 0 | 0 | 0 |
| 01 | 1 | 1 | 1 | 1 |
| 11 | 1 | 1 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 |
Així doncs, l'expressió booleana simplificada per a
A partir d'aquestes tres expressions podem emprar les portes lògiques per crear el circuit digital que implementarà la funció
Exercicis a Jutge.org: Introduction to Digital Circuit Design
Recorda que per accedir als exercicis i perquè el Jutge valori les teves solucions has d'estar inscrit al curs. Trobaràs totes les instruccions aquí.



Xavier Casas, Francesc Madrid
Lliçons.jutge.org
© Universitat Politècnica de Catalunya, 2026
