Sistemes de votació

En el context dels circuits digitals, els sistemes de votació fan referència a implementacions electròniques o lògiques dissenyades per processar múltiples entrades i determinar un resultat basat en una regla de majoria de vots o en una lògica predefinida.

Exemple: Sistema de votació per a comitès

Dissenyarem un sistema electrònic de votació per al Comitè Executiu d'un equip de futbol. Aquest comitè té quatre membres: el President, el Secretari, el Tresorer i el Vocal. Cadascun pot votar Sí (1) o No (0).

Les regles d'aprovació són:

1. Una proposta s’aprova quan tres o més membres voten a favor.
2. En cas d'empat (2 a favor i 2 en contra), el vot del president decideix. Si el president vota "Sí", la proposta s'aprova; si vota "No", es rebutja.

Dissenyarem un circuit lògic amb quatre entrades ($P$, $S$, $T$, $V$) i una sortida ($A$) que indica si la proposta queda aprovada.

Definim les variables d'entrada ($1$ significa "Sí", $0$ significa "No"):

• $P$: vot del President
• $S$: vot del Secretari
• $T$: vot del Tresorer
• $V$: vot del Vocal

La variable de sortida és $A$ (Approved). $1$ significa aprovada, $0$ significa rebutjada.

Analitzem en quins supòsits la proposta serà aprovada, els anomenarem condicions d'aprovació i es deriven de les regles d'aprovació.

Condició 1: Tres o més vots a favor.

Identifiquem totes les combinacions on la suma de P, S, T, V és 3 o 4.

• Aprovat per tres vots a favor
  • $P=0$, $S=1$, $T=1$ i $V=1$ --> ($\overline{P}STV$)
  • $P=1$, $S=1$, $T=1$ i $V=0$ --> ($PST\overline{V}$)
  • $P=1$, $S=1$, $T=0$ i $V=1$ --> ($PS\overline{T}V$)
  • $P=1$, $S=0$, $T=1$ i $V=1$ --> ($P\overline{S}TV$)
• Aprovat per quatre vots a favor
  • $P=1$, $S=1$, $T=1$ i $V=1$ --> ($PSTV$)

La proposta s'aprovarà si es compleix qualsevol d'aquests supòsits (operació OR o suma lògica). La condició 1 s'expressa de la següent manera en l'àlgebra de Boole:

$$C_1=\overline{P}STV+PST\overline{V}+PS\overline{T}V+P\overline{S}TV+PSTV$$

Condició 2: Empat resolt favorablement pel president.

Ens cal identificar totes les combinacions de dos vots a favor i dos en contra. I d'aquestes, ens interessen aquelles amb $P=1$.

• Aprovat
  • $P=1$, $S=1$, $T=0$ i $V=0$ --> ($PS\overline{T}\overline{V}$)
  • $P=1$, $S=0$, $T=1$ i $V=0$ --> ($P\overline{S}T\overline{V}$)
  • $P=1$, $S=0$, $T=0$ i $V=1$ --> ($P\overline{S}\overline{T}V$)
• No aprovat
  • $P=0$ , $S=1$, $T=1$ i $V=0$
  • $P=0$ , $T=0$, $S=1$ i $V=1$
  • $P=0$ , $S=0$, $T=1$ i $V=1$

La proposta s'aprovarà si es compleix algun d'aquests suposits. La condició 2 s'expressa com:

$$C_2=PS\overline{T}\overline{V}+P\overline{S}T\overline{V}+P\overline{S}\overline{T}V$$

La sortida $A$ serà $1$ si es compleix la condició $C_1$ o bé la condició $C_2$. La funció booleana és una suma lògica (OR) d'aquestes dues condicions:

$$A=C_1+C_2$$

I per tant l'expressió de $A$, en funció de $P$, $S$, $T$ i $V$ és:

$$A=\overline{P}STV+PST\overline{V}+PS\overline{T}V+P\overline{S}TV+PSTV+PS\overline{T}\overline{V}+P\overline{S}T\overline{V}+P\overline{S}\overline{T}V$$

Construïm la taula de veritat amb tots els casos possibles:

$P$	$S$	$T$	$V$	Vots favorables	$C_1$	$C_2$	$A$
0	0	0	0	0	0	0	0
0	0	0	1	1	0	0	0
0	0	1	0	1	0	0	0
0	0	1	1	2	0	0	0
0	1	0	0	1	0	0	0
0	1	0	1	2	0	0	0
0	1	1	0	2	0	0	0
0	1	1	1	3	1	0	1
1	0	0	0	1	0	0	0
1	0	0	1	2	0	1	1
1	0	1	0	2	0	1	1
1	0	1	1	3	1	0	1
1	1	0	0	2	0	1	1
1	1	0	1	3	1	0	1
1	1	1	0	3	1	0	1
1	1	1	1	4	1	0	1

L'expressió per a $A$ en funció de $P$, $S$, $T$ i $V$ és molt llarga. Fer-ne una simplificació lògica mitjançant algebra booleana seria complex. Alternativament podem utilitzar un mapa de Karnaugh per a la funció de sortida $A$, amb les entrades $P$,$S$,$T$ i $V$ agrupades.

TV PS	00	01	11	10
00	0	0	0	0
01	0	0	1	0
11	1	1	1	1
10	0	1	1	1

El següent pas és agrupar els ‘1’ en 4 grups, que marcarem amb diferents colors.

TV PS	00	01	11	10
00	0	0	0	0
01	0	0	1	0
11	1	1	1	1
10	0	1	1	1

Les variables constants dins del grup blau són $P=1$ i $T=1$, això es tradueix en el terme $PT$ a la solució.

$$A=PT+···$$

TV PS	00	01	11	10
00	0	0	0	0
01	0	0	1	0
11	1	1	1	1
10	0	1	1	1

Les variables constants en el grup groc són $P=1$ i $V=1$, afegim el terme $PV$ a la solució.

$$A=PT+PV+···$$

TV PS	00	01	11	10
00	0	0	0	0
01	0	0	1	0
11	1	1	1	1
10	0	1	1	1

L’agrupació de color verd té en comú $P=1$ i $S=1$, afegim el terme $PS$ a la solució

$$A=PT+PV+PS+···$$

TV PS	00	01	11	10
00	0	0	0	0
01	0	0	1	0
11	1	1	1	1
10	0	1	1	1

Finalment, en el grup vermell les variables constants són $S=1$, $T=1$ i $V=1$, afegim el terme $STV$ a la solució.

$$A=PT+PV+PS+STV$$

Aquesta és l’expressió booleana simplificada final, perque tots els ‘1’ ja han estat considerats en algun grup.

El circuit digital derivat d’aquesta expressió és el següent:

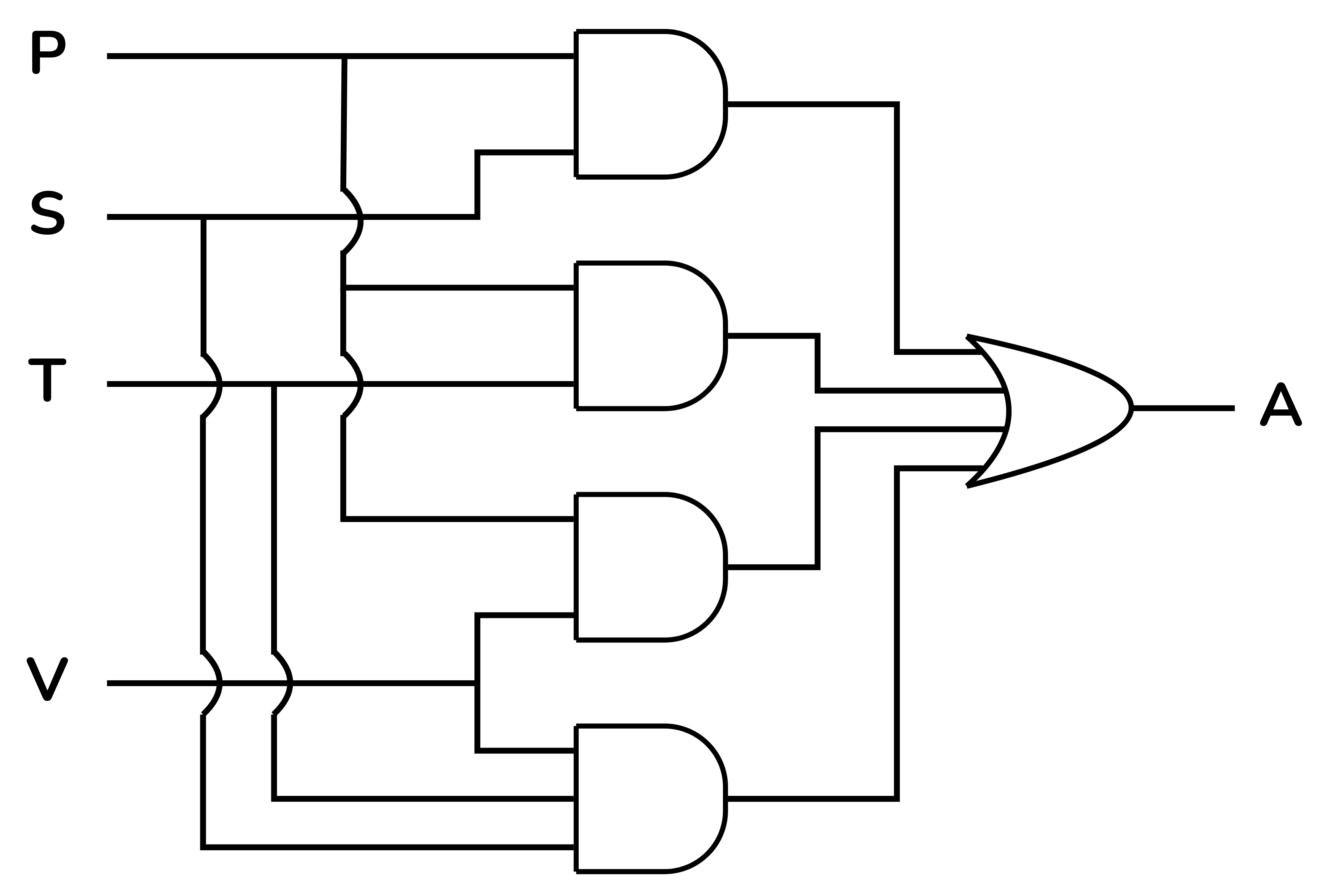
Exercicis a Jutge.org: Introduction to Digital Circuit Design

• Executive Committee
• Two or more ones
• 4-input majority voter
• Majority of 5 inputs

Recorda que per accedir als exercicis i perquè el Jutge valori les teves solucions has d'estar inscrit al curs. Trobaràs totes les instruccions aquí.

Xavier Casas, Francesc Madrid
Lliçons.jutge.org
© Universitat Politècnica de Catalunya, 2025