Application: Calculation of the Euclidean distance between two points

This lesson shows how to write a program that calculates the Euclidean distance between two given points.

Problem statement

We want a program that, given two points, calculates their Euclidean distance. Remember that the Euclidean distance $d$ between two points $(x_1,y_1)$ and $(x_2,y_2)$ can be calculated with the formula:

$$d=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}.$$

Here is its geometric interpretation:

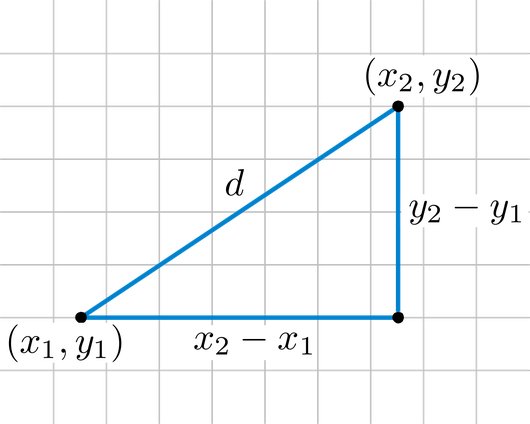
Hey!

Think about how to solve the problem before continuing to read!

Solution

The first step to solving any problem is to identify what its inputs are, what its outputs are, and what relationship they have between them. In this case:

• From the problem statement, it is clear that there are two inputs: the two points. But how are these points represented? Well, with their coordinates. Therefore, the inputs are four real numbers x1, y1, x2, and y2.

• Likewise, it is clear that the output is a real number d that represents the Euclidean distance between the two points.

The relationship between the inputs x1, y1, x2, y2 and the output d is the Euclidean distance formula.

The solution must therefore perform three tasks, one after the other:

1. Read the coordinates x1, y1, x2, y2 of the two points. These coordinates must be real numbers (with decimals).

2. Calculate the value of d from x1, y1, x2, y2. To do this, use the Euclidean distance formula.

3. Print the value of d.

In Python, this can be coded as follows:

x1 = float(input())
y1 = float(input())
x2 = float(input())
y2 = float(input())
d = ((x2 - x1)**2 + (y2 - y1)**2) ** 0.5
print(d)

This time, the first four lines assign to the variables x1, y1, x2, and y2 the values read from the input. The fifth line assigns to d the relevant value from x1, y1, x2, and y2 by evaluating the expression ((x2 - x1)**2 + (y2 - y1)**2) ** 0.5. The sixth line prints the value of d.

Remember that, in Python, the operator ** is the exponentiation operator. Therefore, x**2 is the same as $x^2$ and x**0.5 is the same as $\sqrt{x}$.