Aplicació: Operacions comuns sobre matrius

Aquesta lliçó presenta alguns exemples d’operacions habituals sobre matrius. En particular, aquesta lliçó considera operacions per:
- Sumar matrius
- Trobar la suma per files més gran
- Transposar una matriu quadrada
- Comprovar si una matriu quadrada és simètrica
- Producte de matrius
És molt recomanable que hagueu llegit prèviament els exemples d’operacions de vectors abans de llegir els de matrius, ja que, per no ser massa repetitius, s’ometran alguns detalls ja vistos.
Introducció
Al llarg d’aquesta lliçó suposarem que ja tenim el context següent, que inclou les definicions necessàries i defineix un tipus per a les matrius d’enters i per les seves files:
#include <iostream>
#include <vector>
using namespace std;
using Fila = vector<int>;
using Matriu = vector<Fila>;
Per simplicitat, també entendrem que les matrius amb les que treballarem tenen
com a mínim una fila (encara que sigui buida), ja que si no no té sentit parlar
de columnes i les crides del tipus M[0].size() provocarien un error.
Suma de matrius
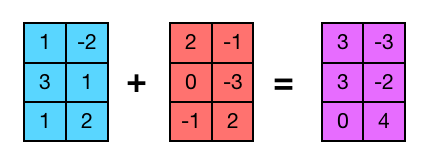
Una de les operacions més bàsiques que es poden fer entre matrius és sumarles. Com sabreu, per poder sumar dues matrius cal que aquestes tinguin les mateixes dimensions, i la suma es realitza element a element. Per comprovar que les dimensions coincideixen, podem fer ús d’asserts, com ja es va explicar a la lliçó del producte escalar, però ara no entrarem en aquest tema i suposarem que les matrius que entrem tenen les dimensions correctes.
Així, una funció que retorna la matriu resultat de sumar dues matrius donades tindria l’aspecte següent:
// retorna la suma de A i B, suposant que tenen la mateixa mida
Matriu suma(const Matriu& A, const Matriu& B)
{
int n = A.size(); // nombre de files
int m = A[0].size(); // nombre de columnes
Matriu C(n, Fila(m)); // resultat
// suma element a element
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
C[i][j] = A[i][j] + B[i][j];
}
}
return C;
}
Com ja s’ha explicat a la lliçó de matrius, ens interessa passar les matrius d’entrada per referència constant, per millorar l’eficiència del programa.
Trobar la suma per files més gran
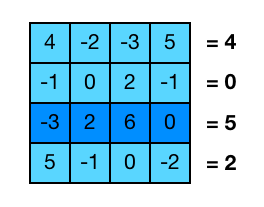
Hi ha molts exemples bàsics d’operacions amb matrius com trobar la suma dels seus elements, la mitjana, el valor i la posició de l’element més gran, etc. Però la majoria d’aquestes són exactament les mateixes que hem fet ja amb vectors, així que les ometrem i presentarem un exemple una mica diferent però senzill que barreja sumes i màxims.
En general, per calcular la suma de certs element donats creem una variable auxiliar inicialment nul·la a la que anem afegint els valors que volem sumar. Per altra banda, per trobar un màxim, creem una altra variable que en tot moment guarda l’element més gran que s’ha trobat fins ara i es va comparant amb els següents. Combinant ambdues estratègies, la nostra funció quedaria així:
// retorna el màxim de les sumes de les files de M
int maxima_suma_fila(const Matriu& M)
{
int n = M.size();
int m = M[0].size();
int suma_max;
for (int i = 0; i < n; ++i) {
// sumar els elements de la fila actual
int suma_act = 0;
for (int j = 0; j < m; ++j) {
suma_act += M[i][j];
}
// si es supera el màxim o és la 1a fila, actualitzem
if (i == 0 or suma_act > suma_max) {
suma_max = suma_act;
}
}
return suma_max;
}
Transposar una matriu quadrada
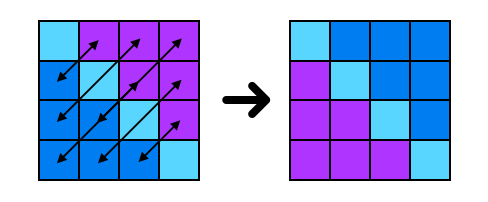
Considerem ara el problema de transposar una matriu quadrada.
Aquest és molt semblant a l’exemple de girar un vector. En aquest cas, els
elements que voldrem intercanviar són el d’índex [i][j] amb el
d’índex [n - 1 - i][n - 1 - j] on n és el nombre de files i columnes. En aquest cas, el que
hem de tenir en compte és que els elements de la diagonal no cal tocar-los i que
només cal visitar una de les dues meitats separades per la diagonal, ja que en
cas contrari recuperarem la matriu inicial perquè farem cada intercanvi dos
cops. L’acció quedaria així:
// transposa la matriu quadrada M
void transposar(Matriu& M)
{
int n = M.size();
for (int i = 1; i < n; ++i) { // per cada índex fila
for (int j = 0; j < i; ++j) { // per cada columna per sota de la diagonal
intercanvia(M[i][j], M[n - 1 - i][n - 1 - j]);
}
}
}
Comprovar si una matriu quadrada és simètrica
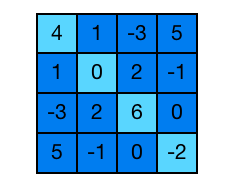
Ara volem comprovar si una matriu quadrada és simètrica o no.
Aquest exemple és pràcticament igual a l’exemple anterior, amb la diferència que en aquest cas no s’han de permutar els elements, sinó que s’han de comparar. La matriu serà simètrica si cada parella d’elements oposats són iguals, o dit d’una altra manera, si hi ha dos elements oposats diferents no serà una matriu simètrica.
Ens quedarà doncs la funció següent que realitza una cerca d’elements simètrics diferents:
bool es_simetrica(const Matriu& M)
{
int n = M.size();
for (int i = 1; i < n; ++i) { // per cada índex fila
for (int j = 0; j < i; ++j) { // per cada columna per sota de la diagonal
if (M[i][j] != M[n - 1 - i][n - 1 - j]) {
return false; // si hi ha 2 diferents no és simètrica
}
}
}
return true; // si no hi ha cap parella diferent és simètrica
}
Producte de matrius

En matemàtiques, donades dues matrius $A$ i $B$, el primer que necessitem per definir el producte $AB$ és que la matriu $A$ tingui exactament el mateix nombre de columnes que el nombre de files de la matriu $B$. En aquest cas, si $A$ és una matriu $n \times m$ i $B$ una matriu $m \times r$, el seu producte serà una matriu $C$ de mida $n \times r$ tal que el seu element $c_{ij}$ (element que es troba a la fila $i$ i columna $j$) es calcula com:
$ c{ij} = \sum{k=1}^m a{ik}b{kj} $
Reproduim ara el procediment anterior amb llenguatge informàtic: Pensem ara quina
forma haurà de tenir el codi d’aquesta funció. Si anomenem les dimensions
de les matrius com ho hem fet a l’apartat anterior, per recórrer la matriu resultat
necessitarem dos bucles (de n i r iteracions, respectivament), i per calcular
cadascun dels seus elements haurem de fer un altra bucle per calcular la suma
dels m elements corresponents. El codi resultant seria aquest:
// retorna el producte de dues matrius A i B de mides compatibles
Matriu producte(const Matriu& A, const Matriu& B)
{
int n = A.size();
int m = B.size(); // o també m = A[0].size()
int r = B[0].size();
Matriu C(n, vectorD(r)); // inicialitzar C a tot zeros
for (int i = 0; i < n; ++i) { // files de C i files de A
for (int j = 0; j < r; ++j) { // columnes de C i columnes de B
for (int k = 0; k < m; ++k) { // columnes de A i files de B
C[i][j] += A[i][k] * B[k][j];
}
}
}
return C;
}

 Lliçons.jutge.org
Lliçons.jutge.org
Rafah Hajjar, Jordi Petit
Universitat Politècnica de Catalunya, 2023
Prohibit copiar. Tots els drets reservats.
No copy allowed. All rights reserved.