Aplicació: Factorial

En aquesta lliçó es calculen els nombres factorials. A més, es presenten el concepte de sobreiximent en operacions amb nombres enters.

Concepte matemàtic del factorial

Donats $n$ objectes, de quantes maneres es poden posar un rera l’altre?

Per exemple, si tenim tres bales, una verda, una blava i una vermella, hi ha sis maneres de posar-les en fila:

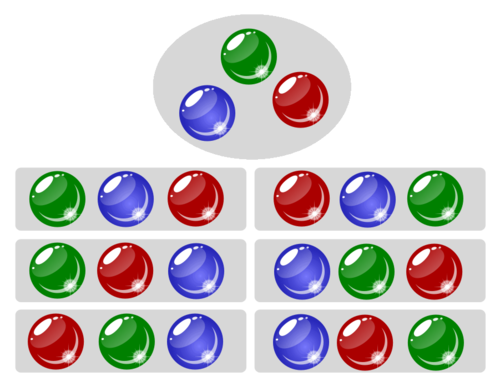
En general, hi ha $n!$ maneres de posar $n$ objectes l’un rera l’altre. Aquí, $n!$ denota el factorial de $n$, definit com

$n!=n(n-1)(n-2)\cdots 1.$

La raó és aquesta: D’entre els $n$ objectes, hi ha $n$ possibilitats de triar-ne un com a primer. Un cop triat aquest primer objecte, en queden $n-1$, i tenim $n-1$ possibilitats de triar-ne un segon, … I així fins a l’últim, on només tenim una possibilitat.

Per definició, $0!=1$. Aquest valor és adequat, ja que hi ha exactament una seqüència amb zero objectes: la seqüència buida.

La taula següent mostra els primers valors dels factorials:

$n$	$n!$
0	1
1	1
2	2
3	6
4	24
5	120

Funció per al factorial

Definim ara una funció en C++ per calcular el factorial d’un natural donat. La capçalera podria ser la següent:

// Retorna el factorial d'un natural n.
int factorial(int n);

És a dir, el nom de la funció és factorial, té un sol paràmetre enter anomenat n, i retorna un enter. A més, hem pres cura d’indicar que n ha de ser un natural, ja que el factorial dels enters negatius no està ben definit.

El cos de la funció és fàcil d’escriure:

// Retorna el factorial d'un natural n.
int factorial(int n) {
    int f = 1;
    for (int i = 1; i <= n; ++i) f = f*i;
    return f;
}

Aquesta funció calcula el factorial de n tot multiplicant una variable f per i, per a tots els i entre 1 i n. Fixeu-vos que factorial(0) retorna 1, tal com cal.

Exercicis

Exercici 1. Considereu aquesta nova versió de factorial on la i s’inicialitza a 2 en lloc d’1:

// Retorna el factorial d'un natural n.
int factorial1(int n) {
    int f = 1;
    for (int i = 2; i <= n; ++i) f = f*i;
    return f;
}

Exercici 2. Considereu ara aquesta nova versió de factorial amb un control diferent del bucle for:

// Retorna el factorial d'un natural n.
int factorial2(int n) {
    int f = 1;
    for (int i = n; i > 1; --i) f = f*i;
    return f;
}

Exercici 3. Considereu finalment una altra versió de factorial:

// Retorna el factorial d'un natural n.
int factorial3(int n) {
    int f = n;
    for (int i = n - 1; i >= 2; --i) f = f*i;
    return f;
}

Problemes de sobreixement

Aquest és un programa complet que escriu una taula amb factorial(n) per a tots els valors d’n entre 0 i 20:

#include <iostream>
using namespace std;

// Retorna el factorial d'un natural n.
int factorial(int n) {
    int f = 1;
    for (int i = 1; i <= n; ++i) f = f*i;
    return f;
}

int main() {
    for (int n = 0; n <= 20; ++n) cout << n << " " << factorial(n) << endl;
}

Si proveu d’executar aquest programa (ho feu sempre, oi?), veureu que la sortida possiblement és

0 1
1 1
2 2
3 6
4 24
5 120
6 720
7 5040
8 40320
9 362880
10 3628800
11 39916800
12 479001600
13 1932053504
14 1278945280
15 2004310016
16 2004189184
17 -288522240
18 -898433024
19 109641728
20 -2102132736

Per als valors d’n més grans que 14, els resultats són incorrectes! 😱! Què passa?

El nostre algorisme és correcte. El problema és que els valors que es poden emmagatzemar en el tipus int estan limitats. Per exemple, en els nostres ordinadors actuals, els valors que es poden representar dins dels enters sovint es troben entre -2147483648 i 2147483647. Com que la funció factorial creix molt ràpid, de seguida es sobrepassen aquests límits i els resultats esdeven incorrectes. Es diu que tenim un sobreiximent. Vegeu la referència sobre els enters per a més informació.

En la majoria dels exemples que veurem en aquest curs, ignorarem el problema dels sobreiximents.

Lliçons.jutge.org
Jordi Petit, Salvador Roura
Universitat Politècnica de Catalunya, 2023