Introducció

Aquesta lliçó presenta uns primers conceptes fonamentals: computadors, dades, programes, algorismes, llenguatges de programació, bugs, problemes, especificacions, … de tot!
Si aquesta primera lliçó us fa mandra o la trobeu complicada, no patiu. Contineu endavant i torneu-hi més endavant. Les coses quedaran més clares.
Computador, dades, programes, llenguatges i algorismes
Un computador és una màquina que processa dades tot aplicant una sèrie d’instruccions elementals. A partir d’unes dades d’entrada subministrades per un usuari, el computador realitza una sèrie de càlculs i genera unes dades de sortida que són lliurades a l’usuari. Els càlculs que executa el computador segueixen un programa que codifica, utilitzant un llenguatge de programació, un algorisme. Un algorisme descriu en detall i sense ambigüitats com resoldre un problema determinat, és a dir, com partir d’unes dades i arribar a unes altres.
Problemes computacionals
Un problema computacional és una pregunta genèrica que es pretén contestar de forma automàtica amb un computador. Les dades que cal subministrar a una pregunta genèrica per tal de poder-la respondre s’anomenen dades d’entrada (o entrades). Les dades corresponents a la resposta s’anomenen dades de sortida (o sortides). Un problema computacional estableix de forma general quines són les dades d’entrada admissibles i quina és la relació entre les dades d’entrada i les dades de sortida.
Exemple: Producte de nombres
Per exemple, “Donats dos naturals $x$ i $y$, quin és el producte de $x$ per $y$?“ és un problema computacional. Aquesta és una pregunta genèrica, en el sentit que no es pot contestar fins que no s’aportin unes dades específiques, i que la resposta, també específica, depèn d’aquestes dades. Així, per exemple, un cop s’indiqui al computador que $x$ val 12 i $y$ val 3, aquest podrà resoldre el problema computacional sobre aquestes dades específiques i respondre que el seu producte és 36. Si s’indica que $x$ val 2891 i $y$ val 4591, llavors la resposta del problema genèric per aquestes dades específiques serà 13272581.
Per aquest problema computacional, les dades d’entrada són, doncs, dos naturals $x$ i $y$, i la única dada de sortida és un altre natural, diguem-ne $p$. La relació entre les dades d’entrada i les dades de sortida és que $p$ ha de ser el producte de $x$ i $y$, és a dir, $p=x·y$.
Exemple: Resolució de Sudokus
Resoldre Sudokus és un altre exemple de problema computacional. Recordeu que el Sudoku és un joc que consisteix a completar una graella 9 × 9 amb números entre 1 i 9 de manera que el resultat final no tingui números repetits a la mateixa fila, columna o submatriu 3 × 3. Aquest és un Sudoku i la seva solució:
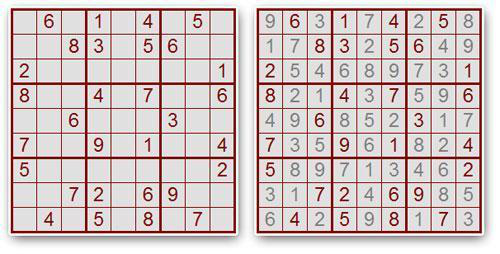
El problema computacional del Sudoku té com a entrada una graella incompleta i té com a sortida una graella completa. La relació entre les dades d’entrades i les de sortida és que la graella de sortida ha de ser comforme amb la graella d’entrada i les regles del joc. Les dades d’entrada admissibles són aquelles que tenen exactament una solució.
Altres exemples
Altres exemples de problemes computacionals inclouen:
Donat un natural, és un nombre primer?
Per a aquest problema, les dades d’entrada són un únic natural, diguem-ne $n$. La dada de sortida és
síquan $n$ és un nombre primer, onoquan $n$ no ho és.En el cas que l’entrada sigui 17, la sortida associada és
sí. En canvi, en el cas que l’entrada sigui 33, la sortida associada ésno.Donada una data vàlida a partir del dia, més i any, quin dia de la setmana li correspon?
Per aquest problema, l’entrada és una data, que es pot representar a través de tres nombres (el dia, el més i l’any). La sortida és un dia de la setmana (dilluns, …, diumenge). Es recalca que la data ha de ser vàlida, perquè altrament la pregunta no té sentit.
Així, en el cas que l’entrada fós 17 11 2006 (el 17 de novembre de 2006), la sortida corresponent seria divendres. En canvi, l’entrada 30 2 2008 (el 30 de febrer de 2008) no és admissible per aquest problema, perquè el febrer no té 30 dies. Determinar si una data és vàlida o no seria un altre problema computacional.
Donat un conjunt no buit de naturals, quin d’ells és el màxim?
Per aquest problema, l’entrada és un conjunt de naturals i la sortida és un dels naturals d’aquest conjunt, concretament el més gran. En aquest cas, cal recalcar que el conjunt d’entrada no pot ser buit, perquè el màxim d’un conjunt buit no està ben definit.
En el cas que l’entrada sigui el conjunt {5,74,-2,11,71}, la sortida associada és l’enter 74. El conjunt buit (∅) no és una entrada admissible d’aquest problema i, per tant, no té cap sortida associada.
Donat un text i un patró, determinar si el patró apareix o no dins del text (i on si hi apareix).
Aquest problema apareix en moltes aplicacions: Per exemple, un usuari d’un processador de textos pot voler buscar una paraula dins del seu document, potser per remplaçar-la per una altra. També, un biòleg pot voler saber si una seqüència de nucleotids apareix o no en una cadena d’ADN. I també, un cercador d’internet tipus Google té interès en trobar una determinada paraula introduïda per un usuari en bilions de pàgines web.
Malgrat totes aquestes diferents aplicacions, les entrades d’aquest problema sempre són dues informacions textuals i la sortida és
síono(i en el cas afirmatiu, on).Així, si tenim una entrada on el text és
esperançai el patró éspera, la sortida associada éssí, començant a la posició 3.
Donada la descripció de les línies i parades del metro d’una ciutat, una estació de partida i una estació de destí, trobar el camí més ràpid per anar del estació d’orígen al estació de destí.
Aquest problema, té com a dades d’entrada un graf (on els vèrtexs corresponen a parades i les arestes a trams entre parades amb l’anotació del seu temps) i dos vèrtexs d’aquest graf. Les dades de sortida són una sèrie de trams a recórrer, començant al vèrtex de partida i acabant al vèrtex de destí, que segueixen els trams de vies, i que formen el camí més ràpid d’entre tots els possibles.
Exercici. Per als problemes següents, identifiqueu quines són les entrades, quines són les sortides, quines condicions han de complir les entrades per ser admissibles, i quina relació hi ha entre les entrades i les sortides.
- Calcular la suma de dos nombres reals.
- Calcular el quocient de dos nombres reals.
- Calcular el quocient i el residu de dos nombres enters.
- Calcular el valor absolut d’un nombre real.
- Calcular l’arrel quadrada d’un nombre real.
- Resoldre una equació lineal.
- Resoldre una equació de segon grau.
- Trobar la mitjana de les notes dels alumnes d’una classe.
- Calcular la distància entre dos punts del pla.
- Calcular la distància entre dos punts de l’espai.
- Esbrinar si dues línies són iguals, paral·leles o s’intersecten.
- Simplificar una fracció.
- Decidir si dues fraccions representen el mateix nombre racional.
Algorismes
Un algorisme és un conjunt explícit d’instruccions per a dur a terme algun càlcul que, a partir d’unes dades d’entrada, produeix unes dades de sortida.

El mot algorisme (o algoritme) prové del nom Abu Abdullah Muhammad ibn Musa al-Khwarizmi, matemàtic i astrònom persa del segle IX que va adoptar el sistema decimal i va desenvolupar els mètodes bàsics de suma, multiplicació i divisió.
Les instruccions que es poden utilizar en un algorisme depenen de les operacions bàsiques que el processador que l’ha d’executar pugui dur a terme. En el cas dels processadors digitals dels computadors moderns, un processador pot realitzar operacions lògiques i aritmètiques, així com encadenar les instruccions una rera l’altra, i executar-ne d’altres condicionalment o repetidament.
Els algorismes es poden expressar usant moltes notacions, incloent llenguatge natural, llenguatges de programació, pseudocodi, diagrames de processos, circuits… En aquest curs, primer esbossarem els algorismes en llenguatge natural, sovint ajudant-nos del llenguatge matemàtic. Després, els concretarem tot utilitzant un llenguatge de programació, Python concretament.
Un algorisme és correcte per a solucionar un determinat problema computacional si, per a totes les possibles dades d’entrada admissibles, les dades de sortida produïdes per l’execució de l’algorisme compleixen l’especificació del problema.
És essencial que els algorismes siguin correctes. Els algorismes incorrectes poden causar que un computador mai doni la resposta (es penji), que executi alguna instrucció il·legal (per exemple, dividir per zero), o que produeixi resultats incorrectes. Depenent del context, els algorismes incorrectes poden provocar efectes catastròfics. Per exemple, la Therac-25 era una màquina de radiacions terapèutiques controlada per computador. La seva mala programació va causar sis accidents entre 1985 i 1987, en els quals els pacients van rebre sobredosis massives de radiació. Tres dels sis pacients en van morir. Un altre error més recent sense conseqüències tant terribles però que afecta molta més gent és la de la primera versió de l’Excel 2007 de Microsoft, que mostra incorrectament el resultat de multiplicar 77.1 per 850: enlloc de donar la resposta 65535, escriu 100000.
A continuació presentem alguns exemples d’algorismes.
Algorisme de multiplicació escolar
Considerem el problema computacional següent: donats dos nombres $x$ i $y$, es vol obtenir el seu producte. Per centrar la discussió, restringim-nos al cas on els dos nombres són naturals (en informàtica, es considera que els nombres naturals inclouen el zero: $\mathbb{N}=\{0, 1, 2, 3, …\}$).
Per resoldre aquest problema, a l’escola ja ens van ensenyar un algorisme quan erem ben petits… Segur que el recordeu! L’aplicació d’aquest algorisme als nombres $x$=2891 i $y$=4591, dóna lloc al desenvolupament següent:
2 8 9 1
× 4 5 9 1
-----------------
2 8 9 1
2 6 0 1 9
1 4 4 5 5
1 1 5 6 4
-----------------
1 3 2 7 2 5 8 1
Fixeu-vos que per poder aplicar aquest algorisme, cal que el processador que el du a terme conegui les taules de multiplicació i sàpiga sumar.
Exercici. Descriviu, en les vostres pròpies paraules però en tot detall, l’algorisme de multiplicació escolar.
Exercici. Complementeu l’explicació anterior per tenir en compte possibles enters negatius.
Algorisme de multiplicació del pagès rús
L’algorisme anterior per multiplicar dos nombres és segurament el més popular (tot i que hi ha països on s’ensenya fent correr les files cap a la dreta enlloc de cap a l’esquerra). Però hi ha altres algorismes ben diferents per multiplicar dos nombres. A continuació considerem l’algorisme de multiplicació del pagès rús (també anomenat multiplicació egípcia, perquè es remonta a la forma per multiplicar que tenien els antics egipcis cap al 2000 aC):
- Utilitzeu una taula amb dues columnes.
- Escriviu els dos nombres a multiplicar ($x$ i $y$) a la primera fila.
- Escriviu els resultats de dividir successivament $x$ entre 2 (oblidant fraccions) a la primera columna, fins que arriveu a 1.
- Escriviu els resultats de multiplicar successivament $y$ per 2 a la segona columna tantes vegades com heu dividit $x$ per 2.
- Marqueu tots els nombres de la segona columna que estan al costat d’un nombre senar a la primera.
- Sumeu tots els nombres de la segona columna que hagueu marcat. Aquest és el resultat de $x$ per $y$.
Apliquem aquest algorisme sobre les dades d’entrada $x$=2891 i $y$=4591:
2891 4591
--------------------
1445 9182 ←
722 18364
361 36728 ←
180 36728
90 146912
45 293824 ←
22 587648
11 1175296 ←
5 2350592 ←
2 2350592
1 9402368 ←
--------------------
13272581
Afortunadament, aquest algorisme dóna la mateixa resposta que el que vam aprendre a l’escola!
Fixeu-vos que per poder aplicar aquest algorisme, el processador que el du a terme ha de saber calcular la meitat d’un nombre, sumar dos nombres i determinar si un nombre és senar. Segur que hauríeu preferit que us ensenyéssin aquest algorisme a l’escola: estudiar les taules de multiplicació costava molt…
Exercici. Utilitzeu l’algorisme de multiplicació del pagès rus per multiplicar 47532 per 1735.
Exercici. Argumenteu perquè l’algorisme de multiplicació del pagès rus és correcte.
Algorisme d’Euclides pel MCD
El màxim comú divisor (MCD) de dos naturals no nuls és el natural més gran que divideix ambdós nombres sense deixar residu. Denotem per $\mcd(a,b)$ el màxim comú dividor de $a$ i de $b$. Per exemple, $\mcd(78,24)=6$ i $\mcd(4,14)=2$.
Una aplicació del màxim comú divisor és la reducció de fraccions: Per exemple, com que $\mcd(78, 24)=6$, tenim
$ \frac{78}{24}=\frac{13·6}{4·6}=\frac{13}{4}. $
Una manera possible per trobar el màxim comú divisor de dos nombres és calcular els divisors de tots ells i quedar-se amb el més gran dels comuns. Una altra manera de trobar el màxim comú divisor de dos nombres és descompondre cadascun d’ells en el seu producte de factors primers, i triar aquells factors que apareguin a les dues descomposicions. Per exemple, per calcular $\mcd(78,24)$, trobem que $78 = 13·3·2$ i que $24 = 3·2·2·2$. Els factors comuns són el 3 i el 2 (tots dos un sol cop), per tant, $\mcd(78,24)=3·2=6$. Tot i que aquests algorismes són correctes, a la pràctica, resulten massa lents i complicats.

Una alternativa millor és utilitzar l’algorisme d’Euclides. Aquest algorisme descobert pels grecs clàssics va ser descrit per Euclides en els seu llibre Elements cap a l’any 300 aC. Molts historiadors consideren que l’algorisme d’Euclides és el primer algorisme de ple dret. Tot i que Euclides va formular el seu algorisme geomètricament, aquí l’interpretarem de forma numèrica. Essencialment, l’algorisme d’Euclides diu:
Resteu al més gran dels dos nombres el més petit, fins que siguin iguals; aquesta és la solució.
Provem de seguir el funcionament d’aquest algorisme per calcular el màxim comú divisor de 78 i 24:
- Al principi, els dos nombres són 78 i 24. Com que el més gran és 78 i el més petit és 24, al 78 li restem 24, quedant ara aquest com 54. L’altre nombre no s’ha tocat, i queda encara com 24.
- Ara, com que 54 i 24 no són iguals, i com que el més gran és 54 i el més petit és 24, al 54 li restem 24, quedant aquest com 30. Els nombres que tenim ara són, doncs, 30 i 24.
- Continuem, perquè 30 i 24 no són encara iguals. Ara toca restar 24 a 30, quedant 6 i 24.
- Com que 6 i 24 no són encara iguals, i el més gran és ara el segon, restem 6 a 24, quedant-nos 6 i 18.
- De nou, com que 6 i 18 no són iguals, restem 6 a 18, i ens queda 6 i 12.
- Com que 6 i 12 no són iguals, restem 6 a 12, i ens queda 6 i 6.
- Ara els dos nombres són iguals (6). L’algorisme ens diu que el nombre obtingut és el màxim comú divisor dels nombres inicials. Per tant, $\mcd(78,24)=6$.
Podem resumir l’execució dels passos anteriors utilitzant una taula de dues columnes. A la primera fila col·locarem els dos nombres dels quals volem calcular el seu màxim comú divisor. A continuació, mirarem quin dels dos és més gran i, a la fila inferior, li restarem el més petit. El més petit el deixarem tal qual. Quan arribem a una fila amb els dos valors iguals, l’algorisme d’Euclides ens diu que aquell nombre és la solució:
78 24
--------
54 24
30 24
6 24
6 18
6 12
6 6
--------
6
Aplicar l’algorisme d’Euclides és ben senzill: només cal considerar sempre dos nombres (que van canviat), cal poder saber si són iguals o no, cal saber també comparar-los per esbrinar quin és el gran i quin és el petit, i cal saber restar-ne un a l’altre.
La correctesa de l’algorisme d’Euclides es basa en la propietat següent:
Propietat. Si $x$ i $y$ són enters estrictament positius tals que $x>y$, llavors $\mcd(x,y)=\mcd(x-y, y)$.
Demostració. Qualsevol enter que divideixi $x$ i $y$ també ha de dividir $x-y$. Per tant, $\mcd(x,y)\le\mcd(x-y, y)$. D’altra banda, qualsevol enter que divideixi $x-y$ i $y$ també ha de dividir $x$ i $y$. Per tant, $\mcd(x-y,y)\le\mcd(x, y)$.
Exercici. Utilitzeu l’algorisme d’Euclides per calcular el màxim comú divisor de 4290 i 910.
Exercici. Què li passa a l’algorisme d’Euclides descrit quan es vol calcular el màxim comú divisor de zero i un altre nombre? Arregleu-ho.
Exercici. Quin és el MCD de 123456789 i 1? Calculeu-lo amb l’algorisme d’Euclides. O… millor que no. Més endavant veurem com arreglar-ho.
Exercici. El mínim comú múltiple de dos naturals és el menor natural (diferent de zero) que és múltiple d’ambdós. Doneu un algorisme per calcular el mínim comú múltiple de dos naturals utilitzant la seva descomposició en producte de factors primers. Doneu una manera de calcular el mínim comú múltiple de dos naturals coneixent el seu màxim comú divisor. Expliqueu com utilitzar el mínim comú múltiple de diferents nombres per sumar fraccions amb denominadors diferents.
Model abstracte de computador
Per tal de poder programar computadors, ens cal saber què és un computador. Ara bé, els computadors moderns són màquines molt complicades i donar-ne una descripció acurada és massa difícil. Per això, nosaltres ens acontentem amb descriure un model abstracte i ideal de computador. Tot i ser un model molt simplificat, aquest conté els elements que més ens interessen a l’hora de començar a programar.
Un computador és una màquina que manipula dades tot aplicant una sèrie d’instruccions d’acord amb un programa. El model de computador abstracte que considerem es compon dels elements següents:
Memòria: La memòria és el lloc on s’emmagatzemen (desen) les dades que manipula l’ordinador. Aquestes dades solen ser nombres, lletres, paraules o combinacions d’aquestes.
Unitat de càlcul: La unitat de càlcul és el lloc on es realitzen les operacions elementals que el computador sap dur a terme. Aquestes operacions poden ser sumar, multiplicar o comparar nombres, per exemple. Les dades que s’operen provenen de la memòria, i els resultats es desen també a la memòria.
Unitat de control: La unitat de control és l’encarregada d’encadenar les instruccions l’una rera l’altra, tot seguint la lògica del programa. Gràcies a la unitat de control certes instruccions es poden repetir, executar o no, etc.
Dispositius d’entrada/sortida: Els dispositius d’entrada/sortida (E/S) asseguren la comunicació del computador amb l’exterior; serveixen per introduir les dades d’entrada i extreure les dades de sortida. Per simplicitat, considerem que només hi ha un sol dispositiu d’entrada i un sol dispositiu de sortida. El dispositiu d’entrada llegeix dades que desa a la memòria; el dispositiu de sortida escriu dades emmagatzemades a la memòria.
Si pensem en un ordinador corrent d’avui en dia, la memòria es correspon a la seva RAM (el meu ordinador té 16 gigabytes de memòria), les unitats de càlcul i de control es corresponen al seu processador (el meu ordinador té un Intel Core de 3.1 a gigahertzs, i els dispositius d’entrada/sortida es corresponen als dispositius que hi connectem (per exemple, el teclat, el ratolí i el micròfon són dispositius d’entrada; el monitor i l’impressora són dispositius de sortida; i els discos durs i la connexió de xarxa són d’entrada i sortida).
Com és evident, tots aquests elements són molt complexes, però els sistemes operatius ens permeten considerar-los d’una forma molt més senzilla. El sistema operatiu d’un computador és el programari que gestiona els recursos del computador i ofereix serveis als programadors per utilitzar-los tot amagant la seva complexitat. En particular, el sistema operatiu sol oferir serveis per a la gestió de la memòria, dels processos (programes actius) i dels perifèrics (a través de sistemes de fitxers).
Exercici. Esbrineu quin sistema operatiu té el vostre computador personal. Esbrineu també quin processador té, quanta memòria té, i quins són els seus dispositius d’entrada, de sortida i d’entrada sortida.
Exercici. Compteu i enumereu quants dispositius amb un processador digital teniu a casa (ordinadors, mòbils, TVs, …).
Llenguatges de programació
Un llenguatge de programació és un llenguatge artificial per controlar un computador tot expressant de forma precisa un algorisme.
Existeixen milers de llenguatges de programació. A grans trets, aquests es poden classificar segons el seu ús (propòsit general, programació de sistemes, programació de guions), el seu nivell d’abstracció (d’alt, mig o baix nivell) i segons el seu paradígma de programació (imperatiu, funcional o lògic).
Els llenguatges de programació es defineixen a través d’unes regles sintàctiques (com s’escriuen les coses) i d’unes regles semàntiques (què descriuen les coses).
Com que els computadors no enténen directament els llenguatges de programació, cal primer convertir un programa escrit en un llenguatge de programació concret en les instruccions bàsiques que realment entén el computador. Aquest procés s’anomena compilació. Per fortuna aquesta conversió la pot fer automàticament el propi computador a través d’un programa anomenat compilador, el qual també aprofita la ocasió per verificar que el programa no contingui errors sintàctics ni semàntics.
Nosaltres ens centrem en els llenguatges de programació imperatius. En un llenguatge imperatiu, un programa consisteix en una sèrie d’instruccions que descriuen canvis en les dades de la memòria. En aquest curs programem els algorismes utilitzant el llenguatge Python. Aquest llenguatge de programació és enorme; només en veurem una petita part, tot destacant les construccions que la majoria dels llenguatges imperatius comparteixen amb ell. A la propera lliçó veurem com començar a treballar en Python.
Desenvolupament de programes
El procés de desenvolupament d’un programa involucra realitzar les etapes següents:
Especificació del problema: El primer pas que cal fer és especificar quin és el problema a resoldre. Especificar un problema consisteix en descriure adecuadament el problema considerat. Per això cal descriure quines són les seves possibles dades d’entrada, quines són les possibles dades de sortida i quina relació hi ha entre les dades de sortida i les dades d’entrada. Això involucra comprendre tot el context del problema. En l’etapa d’especificació es tracta només de què cal arribar a fer, no de com fer-ho.
Disseny d’un algorisme: A continuació, cal dissenyar un algorisme per solucionar el problema. Dissenyar un algorisme és una tasca molt creativa, lligada a l’experiència i al coneixement de diversos esquemes algorísmics.
Codificació d’un programa: Després, cal escriure un programa tot codificant l’algorisme utilitzant un llenguatge de programació. Aquest programa es prepara per tal de poder ésser executat pel computador.
Proves del programa: Finalment, un cop el programa preparat, cal provar-lo. Això consisteix en executar-lo sobre algunes entrades, per tal d’assegurar-se que, almenys sobre aquelles entrades, el programa funciona tal com s’espera.
Malauradament, durant la realització d’aquest etapes, es cometen o diagnostiquen errors que impliquen recular a etapes anteriors. Per això, sempre és convenient deixar ben documentat l’assoliment de cadascuna de les etapes.
La programació és la disciplina que s’encarrega d’escriure, ampliar, provar, corregir i mantenir programes. L’enginyeria de software és la branca de l’informàtica que es preocupa de tots els aspectes de la producció de programes de forma sistemàtica i organitzada.
 Lliçons.jutge.org
Lliçons.jutge.org
Jordi Petit
Universitat Politècnica de Catalunya, 2023
Prohibit copiar. Tots els drets reservats.
No copy allowed. All rights reserved.