Ús de funcions

Aquesta lliçó presenta com usar funcions. A través de funcions predefinides o de funcions importades d’altres mòduls, els nostres programes poden dur a terme tasques més o menys complicades sense haver d’escriure tant de codi i, per tant, amb menys possibilitat d’errors.
Ús de funcions predefinides
Python ofereix un petit repertori de funcions predefinides, és a dir, funcions que es poden utilitzar directament. Una funció té un nom i calcula un valor a partir de certs paràmetres. Les funcions es poden cridar (o invocar) dins de qualsevol expressió, ja que dónen lloc a un valor.
Suposem que volguéssim escriure el màxim de dos nombres desats en les variables a i b. Ja hem vist anteriorment com fer aquesta tasca utilitzant un condicional, però és molt més pràctic utilitzar la funció predefinida max. Per exemple, podríem fer:
m = max(a, b)
o
print(max(a, b))
El càlcul del màxim d’a i de b s’ha relegat ara a la funció predefinida max, la qual probablement implementa internament el condicional igual que l’haguéssim fet nosaltres. Però gràcies a l’ús de la funció, el propòsit del nostre codi és molt més clar.
max és una funció que, donats dos valors, en retorna el més gran. Podem utilitzar la funció max en qualsevol lloc on pugui aparèixer una expressió. Si ens calgués escriure el màxim de tres valors a, b i c, podríem usar dues crides a max d’aquesta forma:
print(max(a, max(b, c)))
Això demostra que el resultar d’un max es pot usar com a valor per a un paràmetre d’un altre max.
Millor encara, podem aprofitar que max pot rebre qualsevol nombre de paràmetres:
print(max(a, b, c))
De forma anàloga, la funció predefinida min calcula el mínim de diferents valors. A més, la funció predefinida abs calcula el valor absolut de nombres:
max(10, 20, 15) 👉 20
min(31, 37, 11) 👉 11
abs(12) 👉 12
abs(-12) 👉 12
abs(-4 * max(1, 3)) 👉 12
De forma semblant la funció predefinida round arrodoneix un real a l’enter més proper. I, si se li dóna un segon paràmetre, aquest indica que cal retornar l’arrodoniment com a un real amb aquell nombre de dígits decimals:
round(4.1) 👉 4
round(4.9) 👉 5
round(3.1111, 2) 👉 3.11
round(3.1991, 2) 👉 3.20
La funció predefinida len serveix per calcular les llargades de diferents objectes. Per textos, en retorna el seu nombre de caràcters:
len('Frank Zappa') 👉 11
len('') 👉 0
I ha moltes més funcions predefinides. Podeu trobar-ne documentació a https://docs.python.org/3/library/functions.html, però crec que les anteriors són les que us poden caldre ara.
Funcions de conversió entre tipus de dades
En ocasions, els programadors necessiten convertir valors d’un tipus en valors d’un altre tipus. Per això, es fa servir la notació tipus(valor), on el nom del tipus s’utilitza com si fos una funció predefinida. Aquestes funcions s’anomenen funcions de conversió. Aquí en teniu alguns exemples:
>>> int(3.1)
3
>>> int(3.9)
3
>>> int('123')
123
>>> float(13)
13.0
>>> float('3.50')
3.5
>>> str(45)
'45'
>>> str(45.5)
'45.5'
>>> bool(666)
True
>>> bool(0) # 0 és l'únic enter que es converteix a fals
False
>>> bool('res')
True
>>> bool('') # '' és l'únic text que es converteix a fals
False
Ús de funcions matemàtiques
El mòdul math és un mòdul estàndard de Python que s’utilitza per treballar amb càlculs científics complexos. Aquest mòdul de matemàtiques ofereix funcions matemàtiques usuals com ara arrodoniments, operacions trigonomètriques, operacions logarítmiques, ètc.
Aquesta és una llista de les funcions més habituals de math:
| Funció | Descripció |
|---|---|
| sin | sinus |
| cos | cosinus |
| tan | tangent |
| asin | arcsinus |
| acos | arccosinus |
| atan | arctangent |
| degrees | conversió de radians a graus |
| radians | conversió de grans a radians |
| sqrt | arrel quadrada |
| pow | potència |
| log | logarítme |
| ceil | arrodoniment cap amunt |
| floor | arrodoniment cap avall |
| trunc | arrodoniment cap amunt per negatius, cap avall per positius |
| factorial | factorial |
| gcd | màxim comú divisor |
Per exemple, suposem que volem calcular la distància entre dos punts del pla $p = (x_p, y_p)$ i $q = (x_q, y_q)$. Recordem que la seva distància euclídea és $\sqrt{(x_p-x_q)^2 + (y_p-y_q)^2}$. El programa següent ho implementa:
from yogi import read
from math import sqrt, pow
xp = read(float)
yp = read(float)
xq = read(float)
yq = read(float)
distancia = sqrt(pow(xp - xq, 2) + pow(yp - yq, 2))
print(distancia)
També hi ha moltes més funcions a la llibreria matemàtica. Podeu trobar-ne la documentació a https://docs.python.org/3/library/math.html. A més, també hi ha una llibreria matemàtica per a nombres complexos, vegeu https://docs.python.org/3/library/cmath.html
A més de funcions, el mòdul de matemàtiques també ofereix constants com ara math.pi (pel nombre π) i math.e (per la constant d’Euler). És important usar aquestes constants per tenir els valors més exactes possibles i no deixar tot de valors màgics 3.1416 en el codi.
Ús de funcions aleatòries
El mòdul estàndard random proporciona funcions relacionades amb la generació de nombres aleatoris (o, més ben dit, de nombres pseudoaleatoris). Aquestes funcions són un xic diferents de les funcions anteriors, en el sentit que no solen retornar el mateix valor cada cop que es criden amb els mateixos paràmetres.
Per exemple, la funció randint retorna un nombre a l’atzar entre dos de donats. Aquestes crides mostren com es pot usar per simular el llençament d’un dau de sis cares:
>>> import random
>>> random.randint(1, 6) # probablement us sortiran valors diferents!
4
>>> random.randint(1, 6) # probablement us sortiran valors diferents!
6
>>> random.randint(1, 6) # probablement us sortiran valors diferents!
1
Si voleu obtenir la suma de dos daus, podeu escriure l’expressió random.randint(1, 6) + random.randint(1, 6). Fixeu-vos que en aquest cas, no voleu escriure 2 * random.randint(1, 6). Enteneu perquè?
La funció random (dins del mòdul random) retorna reals a l’atzar uniformement distribuïts entre 0 i 1:
>>> import random
>>> random.random() # probablement us sortiran valors diferents!
0.21020758023523933
>>> random.random() # probablement us sortiran valors diferents!
0.5707826663140387
I, de forma semblant, la funció uniform retorna reals a l’atzar uniformement distribuïts entre els dos paràmetres donats:
>>> import random
>>> random.uniform(0, 1/3) # probablement us sortiran valors diferents!
0.25364034594325036
>>> random.uniform(0, 1/3) # probablement us sortiran valors diferents!
0.17085249688605977
Com a aplicació, aquest programa visualitza el llençament de 100 punts a l’atzar en un quadrat:
import turtle
import random
punts = 100
mida = 100
# dibuixa el quadrat
for i in range(4):
turtle.forward(mida)
turtle.right(90)
# dibuixa els punts
for i in range(punts):
turtle.penup()
turtle.goto(random.uniform(0, mida), -random.uniform(0, mida))
turtle.pendown()
turtle.dot()
turtle.done()
Aquesta ha estat la sortida obtinguda en una execució:
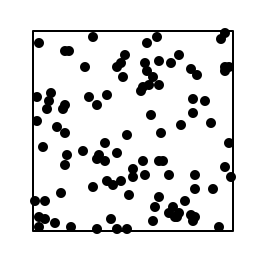
Podeu trobar documentació addicional del mòdul random a https://docs.python.org/3/library/random.html.
Ús de funcions relacionades amb el temps
El mòdul estàndard time proporciona funcions relacionades amb el temps. Per exemple, la funció time del mòdul time (sí, es diuen igual), retorna un real amb el nombre de segons transcorreguts des d’algun moment arbitrari en el passat. És útil per mesurar el temps transcorregut en un fragment de codi calculant la diferència entre els temps després i abans d’aquell fragment:
import time
inici = time.time()
... # fragment codi de codi que volem mesurar
final = time.time()
print('temps transcorregut:', final - inici, 'segons')
 Lliçons.jutge.org
Lliçons.jutge.org
Jordi Petit
Universitat Politècnica de Catalunya, 2023
Prohibit copiar. Tots els drets reservats.
No copy allowed. All rights reserved.